суммы 1 и 4 являются чётными числами
Пошаговое объяснение:
1) 1+2+3+... + 100
Данное выражение представляет собой сумму арифметической прогрессии с a₁ = 1 и d = 1.
Сумма 100 членов данной прогрессии равна
S₁₀₀ = 0.5 · (1 + 100) · 100 = 5050 - чётное число
2) 1+3+5+…+333
Данное выражение представляет собой сумму арифметической прогрессии с a₁ = 1 и d = 2.
Найдём количество членов этой прогрессии
аₙ = 333
333 = 1 + 2 · (n - 1)
332 = 2(n - 1)
n - 1 = 166
n = 167
Сумма 167 членов данной прогрессии равна
S₁₆₇ = 0.5 · (1 + 333) · 167 =27 889 - нечётное число
3) 10+13+16+…+1000
Данное выражение представляет собой сумму арифметической прогрессии с a₁ = 10 и d = 3.
Найдём количество членов этой прогрессии
аₙ = 1000
1000 = 10 + 3 · (n - 1)
990 = 3(n - 1)
n - 1 = 330
n = 331
Сумма 331 члена данной прогрессии равна
S₁₆₇ = 0.5 · (10 + 1000) · 331 = 167 155 - нечётное число
4) 5+10+15+…+555
Данное выражение представляет собой сумму арифметической прогрессии с a₁ = 5 и d = 5.
Найдём количество членов этой прогрессии
аₙ = 555
555 = 5 + 5 · (n - 1)
550 = 5(n - 1)
n - 1 = 110
n = 111
Сумма 111 членов данной прогрессии равна
S₁₁₁ = 0.5 · (5 + 555) · 111 = 31 080 - чётное число
5) 3 + 7 + 11 +... + 83
Данное выражение представляет собой сумму арифметической прогрессии с a₁ = 3 и d = 4.
Найдём количество членов этой прогрессии
аₙ = 83
83 = 3 + 4 · (n - 1)
80 = 4(n - 1)
n - 1 = 20
n = 21
Сумма 21 члена данной прогрессии равна
S₁₆₇ = 0.5 · (3 + 83) · 21 = 903 - нечётное число
всего - 13 монет
комар - по 5 монет - ?
муха - по 2 монеты - ?
1) предположим, что мистер Джобс купил 1 комара, тогда у него останется:
13 - 5 = 8 монет
2) если мистер Джобс купил 2 комара, то у него останется:
8 - 5 = 3 монеты, но такого не может быть по условию, т.к. оставшиеся 3 монеты нечётное число, а мухи стоят по 2 монеты (чётное).
Получается, что мистер Джобс купил 1 комара и у него осталось 8 монет.
3) посчитаем, сколько он купил мух:
8 : 2 = 4 мухи
Если деление еще не проходили, то вычитаем по 2 монеты:
8 - 2 = 6 монет
6 - 2 = 4 монеты
4 - 2 = 2 монеты
2 - 2 = 0 монет
ответ: мистер Джобс купил 1 комара и 4 мухи.
Пошаговое объяснение:
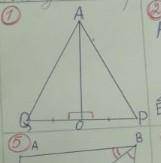
<АОQ=<AOP, так как АО перпендикуляр, по условию.
AO- общая сторона.
QO=OP, по условию
∆АОQ=∆AOP, по первому признаку равенства.