Пошаговое объяснение:
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Используя эту формулу, решается задача 1) и 2) - ответами в обоих будет число 24. Для задачи 3) введем формулу (на картинке), где m - количество элементов в конечной выборке (т.е. то кол-во мужчин, которые садятся на скамейку), а n - кол-во элементов массива(кол-во свободных на скамейке мест). Подставив все величины в формулу, получим :
C =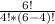 
= 15 возможностей их различной посадки
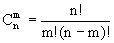
Вместо * можно подставить только цифру 5 (число 41454 делится на 9 без остатка).
Пошаговое объяснение:
Признак делимости на 9: сумма всех цифр числа должна делиться на 9. Обозначим через x пропущенную цифру (0 ≤ x ≤ 9), тогда сумма всех цифр равна 4+1+4+x+4 = 13+x. В интервале (13+0; 13+9) без остатка делится на 9 только число 18, поэтому 13+x=18 и x=5.