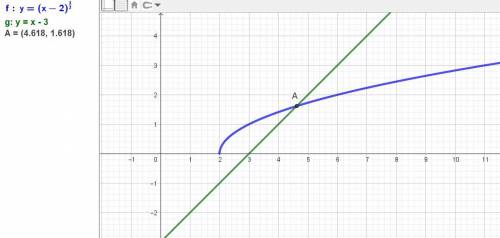
Дано уравнение: √(x - 2) = x - 3.
ОДЗ: х - 2 > 0, x > 2.
Надо обе части уравнения возвести в квадрат.
х - 2 = х² - 6х + 9.
Получаем квадратное уравнение:
х² - 7x + 11 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-7)^2-4*1*11=49-4*11=49-44=5;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√5-(-7))/(2*1)=(√5+7)/2=√5/2+7/2=√5/2+3.5~~4.618034;
x_2=(-√5-(-7))/(2*1)=(-√5+7)/2=-√5/2+7/2=-√5/2+3.5~~2.381966.
Получили 2 корня - это результат лишнего корня при возведении в квадрат, но должна быть одна точка пересечения одной ветви параболы и прямой.
Второй корень не подходит.
ответ: х1 = √5/2+3,5.
72 = 2•2•2•3•3
НОД (126; 72) = 18
18 = 2•3•3
Значит,
а может принимать значения 2; 3; 6; 9; 18
Ну и, разумеется, значение 1.
При а = 1
126/1 = 126
72/1 = 72
При а = 2
126/2 = 63
72/2 = 36
При а = 3
126/3 = 42
72/3 = 24
При а = 6
126/6 = 21
72/6 = 12
При а = 9
126/9 = 14
72/9 = 8
При а = 18
126/18 = 7
72/18 = 4
При всех прочих значениях а дроби не принимают натуральные значения.
ответ: 1; 2; 3; 6; 9; 18.