1) х+4 4/19=6 2/19
х = 6 2/19 - 4 4/19
х = 5 21/19 - 4 4/19
х = 1 17/19
2) х + 2х + х+7 = 39
4х = 39 - 7
4х = 32
х = 32 : 4
х = 8 (см) - одна сторона треугольника.
8 * 2 = 16 (см) - вторая сторона треугольника.
8 + 7 = 15 (см) - третья сторона прямоугольника.
3) Если площадь водохранилища Волгоградского обозначит за Х, то
Х + (Х+1463) + ( Х + 3383) = 14197
3Х = 14197 - 1463 - 3383
3Х = 9351
Х = 9351 : 3
Х = 3117 (км2) - площадь водохранилища Волгоградского.
3117 + 1463 = 4580 (км2) - площадь водохранилища Рыбинского.
3117 + 3383 = 6500 (км2) - площадь водохранилища Куйбышевского.
Во время прочтения смотрите рисунки.
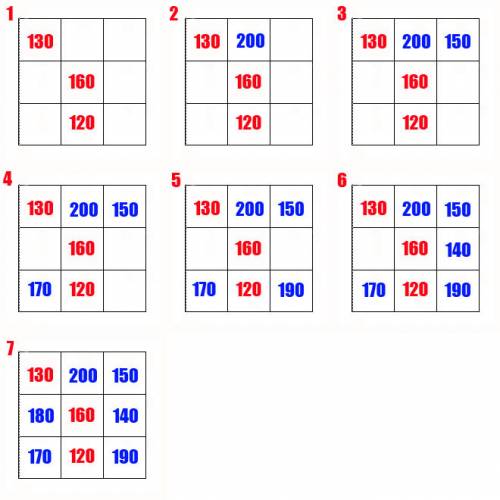
Дано: В магический квадрат вписаны числа 130, 160 и 120 (см. рис. 1). Необходимо вписать ещё следующие числа 200, 150, 180, 140, 170 и 190.
Решение: Определим, какова д.б. сумма по строкам и столбцам, а также по диагонали. Для этого найдём сумму всех чисел и разделим их на 3 (по числу строк или столбцов).
130 + 160 + 120 + 200 + 150 + 180 + 140 + 170 + 190 = 1440
1440 : 3 = 480
Итак, сумма по строкам, столбцам и диагоналям д.б. равна 480. Во втором столбце свободна самая верхняя клетка, а две другие заняты. Значит, мы можем найти число, которое следует вписать в эту клетку: 480 – (160 + 120) = 200 (см. рис. 2).
Теперь можем найти число в правом верхнем углу: 480 – (130 + 200) = 150 (см. рис. 3)
Находим число в левом нижнем углу: 480 – (150 + 160) = 170 (см. рис. 4).
Число в правом нижнем углу можем найти двумя по третьей строке: 480 – (170 + 120) = 190 или по диагонали: 480 – (130 + 160) = 190 (см. рис. 5).
Найдём число на пересечении второй строки и третьего столбца: 480 – (150 + 190) = 140 (см. рис. 6).
Осталось одно число – 180, которое вписываем в оставшуюся пустую клетку (см. рис. 7). Также можно вычислить двумя по второй строке 480 – (160 + 140) = 180, или по первому столбцу 480 – (130 + 170) = 180.
Всё, магический квадрат готов.