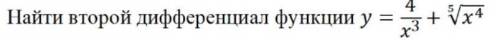
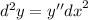
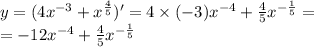
![y = - 12 \times ( - 4) {x}^{ - 5} + \frac{4}{5} \times ( - \frac{1}{5} ) {x}^ { - \frac{6}{5} } = \\ = \frac{48}{ {x}^{5} } - \frac{4}{25x \sqrt[5]{x} }](/tpl/images/4177/3163/3e05a.png)
![{d}^{2} y = ( \frac{48}{ {x}^{5} } - \frac{4}{25x \sqrt[5]{x} } ) {dx}^{2} \\](/tpl/images/4177/3163/d678e.png)
Пусть на острове x участков 10×40 метров и 16-x участков 20×20 метров.
Периметр каждого участка 10×40 метров равен (10+40)·2 = 100 метров, периметр каждого участка 20×20 метров - 20·4 = 80 метров.
Тогда периметр всех участков 100x+80·(16-x) = 100x+1280-80x = 20x+1280 метров.
На берегах острова заборов нет, значит длина всех заборов на 80·4 = 320 метров меньше периметра всех участков.
20x+1280-320 = 20x+960 м - длина всех заборов.
Но так как между двумя соседними участками забор один, выходит, что мы дважды почитали длины всех заборов. Значит суммарная длина всех заборов равна (20x+960):2 или 540 метров

ответ: на острове 6 участков размером 10×40 метров.
Пусть на острове x участков 10×40 метров и 16-x участков 20×20 метров.
Периметр каждого участка 10×40 метров равен (10+40)·2 = 100 метров, периметр каждого участка 20×20 метров - 20·4 = 80 метров.
Тогда периметр всех участков 100x+80·(16-x) = 100x+1280-80x = 20x+1280 метров.
На берегах острова заборов нет, значит длина всех заборов на 80·4 = 320 метров меньше периметра всех участков.
20x+1280-320 = 20x+960 м - длина всех заборов.
Но так как между двумя соседними участками забор один, выходит, что мы дважды почитали длины всех заборов. Значит суммарная длина всех заборов равна (20x+960):2 или 540 метров
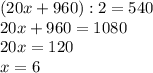
ответ: на острове 6 участков размером 10×40 метров.