1) Пусть первое нечетное число равно , тогда следующее за ним нечетное число равно . Произведение этих двух чисел равно 575. Составим уравнение.
Значит первое число равно 23.
Второе число
Проверка: 23·25=575
ответ: 23 и 25.
2) Диагональ делит прямоугольник на два равных прямоугольных треугольника (см. рисунок). В получившемся прямоугольном треугольнике диагональ является гипотенузой, а стороны прямоугольника катетами.
Пусть один катет равен , тогда второй катет равен . Гипотенуза равна 25.
Чтобы сравнивать дроби, их нужно привести к общему знаменателю. Из двух правильных дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
2/6 и 4/7 = 14/42 и 24/42 Общий знаменатель 42 42 : 6 = 7 - доп.множ. к 2/6 = (2*7)/(6*7) = 14/42 42 : 7 = 6 - доп.множ. к 4/7 = (4*6)/(7*6) = 24/42 2/6 < 4/7, так как 14/42 < 24/42
3/7 и 4/5 = 15/35 и 28/35 Общий знаменатель 35 35 : 7 = 5 - доп.множ. к 3/7 = (3*5)/(7*5) = 15/35 35 : 5 = 7 - доп.множ. к 4/5 = (4*7)/(5*7) = 28/35 3/7 < 4/5, так как 15/35 < 28/35
2/15 и 3/20 = 8/60 и 9/60 Общий знаменатель 60 60 : 15 = 4 - доп.множ. к 2/15 = (2*4)/(15*4) = 8/60 60 : 20 = 3 - доп.множ. к 3/20 = (3*3)/(20*3) = 9/60 2/15 < 3/20, так как 8/60 < 9/60
1) 23 и 25.
2) 7 и 24.
Пошаговое объяснение:
1) Пусть первое нечетное число равно
, тогда следующее за ним нечетное число равно 
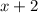. Произведение этих двух чисел равно 575. Составим уравнение.
Значит первое число равно 23.
Второе число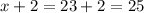
Проверка: 23·25=575
ответ: 23 и 25.
2) Диагональ делит прямоугольник на два равных прямоугольных треугольника (см. рисунок). В получившемся прямоугольном треугольнике диагональ является гипотенузой, а стороны прямоугольника катетами.
Пусть один катет равен
, тогда второй катет равен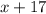 
. Гипотенуза равна 25.
По теореме Пифагора:
Ширина прямоугольника равна 7 см.
Длина прямоугольника равна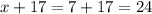
(см)
ответ: 7 см, 24 см.