Пошаговое объяснение:
Вот
Сначала найдём все числа, принадлежащие заданному множеству:
х ∈ N, x² ≤ 40
Расшифровка: х – натуральное число, квадрат которого меньше 40.
Таких чисел не так много, вот они (учитывая, что нуль не принадлежит множеству натуральных чисел):
1 2 3 4 5 6
Из этих шести чисел нужно составлять трёхзначные числа, делящиеся на 5. Очевидно, цифра 5 пойдёт в конец и так там и останется, иначе число не разделится:
* * 5
Отсюда нам нужно просто переставлять наши шесть чисел (от 1 до 6) на первых двух местах.
Необязательно знать правила комбинаторики, чтобы найти правильный ответ, достаточно простых рассуждений:
• любое из шести чисел может стоять на первом месте, что даёт нам шесть вариантов составления числа.
• любое из шести чисел может стоять на втором месте, что даёт нам шесть вариантов для каждого из шести предыдущих вариантов.
Итого: 6 × 6 = 36.
ответ: 36.
Пошаговое объяснение:
Дано:
d = 16 см (диаметр окружности);
l AB l -10 см (длина секущей).
Найти:
Расстояние между прямыми а и в
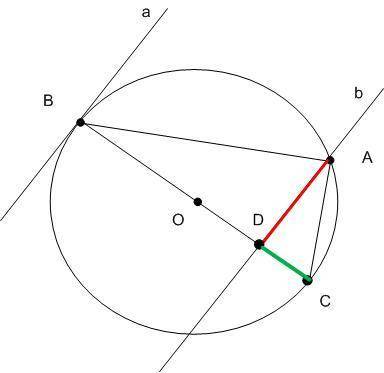
Выполним дополнительные построения (см. рис. "касательная и секущая".
l ВС l = d - диаметр, Δ ABC - прямоугольный, прямой угол ∠А (как треугольник, опирающийся на диаметр).
Найдем величину l AC l (по теореме Пифагора):
l AC l=√(d²- l AB l²);
l AC l=√(16²-10²)=√(256-100)=√156=2√39;
Т.к. прямые а и в параллельны, то ∠ ADB - прямой. И, следовательно,
расстояние между касательной а и секущей в - l BD l равно диаметру окружности минус отрезок l DС l.
l BD l = d - l DС l
Обозначим длину отрезка l DС l через х.
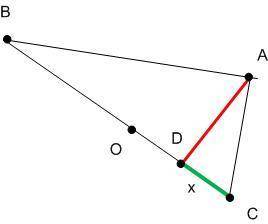
Рассмотрим поближе Δ ABC и Δ ADC (см рис. "подобные треугольники"). Эти треугольники прямоугольные, и, что самое важное, эти треугольники подобные (они имеют равные острые углы. ∠ACD = ∠ACB)!
А, как известно, у подобных треугольников стороны пропорциональны. Составим пропорцию (вспомнив, что против равных углов лежат пропорциональные стороны):
l AC l/x=d/l AC l;
x=l AC l²/d;
x=(2√39)²/16=(4*39)/16=39/4;
l BD l = d - l DС l ⇒ l BD l = d - x;
l BD l =16-39/4=64/4-39/4=25/4=6 1/4=6.25
24
Пошаговое объяснение:
Проверено в билимленде