Пошаговое объяснение:
Рисунок сразу с тремя графиками функций на рисунке в приложении.
В качестве исходного - график Y= cosX.
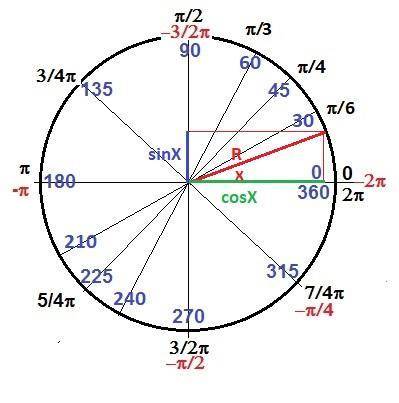
Эта функция от вращения точки по окружности радиусом = 1.
Rx/R = cosX, Ry/R = sinX. - на рисунке в приложении.
И так период функции Y = cosX = 2*π = 360°
Амплитуда значений таких функций не может быть больше R = 1.
Задание 1. Y = cos 2*x
Амплитуда остаётся такой же = 1, а вот период изменился и стал уже не 360°, а 360/2 = 180° = π.
На компьютерных графиках писать π - сложно. 30° = π/6. 60° = π/3.
СВОЙСТВА.
Амплитуда осталась равной единице, сдвига по оси Х - нет, а вот период стал в два раза меньше.
Задача 2 - Y= 1/2*cosX
Здесь совсем малое свойство - амплитуда уменьшается в два раза, па период так и остался - 2π = 360°
ДОПОЛНИТЕЛЬНО
Для построения тригонометрических функций надо запомнить значения функции в основных точках.
Х=0, У = 1
Х = π/3 = 60° У = √3/2 ≈ 0,87
Х = π/6 = 30° У = 0,5
Х = π/2 = 90° У = 0.

Пошаговое объяснение:
Рисунок сразу с тремя графиками функций на рисунке в приложении.
В качестве исходного - график Y= cosX.
Эта функция от вращения точки по окружности радиусом = 1.
Rx/R = cosX, Ry/R = sinX. - на рисунке в приложении.
И так период функции Y = cosX = 2*π = 360°
Амплитуда значений таких функций не может быть больше R = 1.
Задание 1. Y = cos 2*x
Амплитуда остаётся такой же = 1, а вот период изменился и стал уже не 360°, а 360/2 = 180° = π.
На компьютерных графиках писать π - сложно. 30° = π/6. 60° = π/3.
СВОЙСТВА.
Амплитуда осталась равной единице, сдвига по оси Х - нет, а вот период стал в два раза меньше.
Задача 2 - Y= 1/2*cosX
Здесь совсем малое свойство - амплитуда уменьшается в два раза, па период так и остался - 2π = 360°
ДОПОЛНИТЕЛЬНО
Для построения тригонометрических функций надо запомнить значения функции в основных точках.
Х=0, У = 1
Х = π/3 = 60° У = √3/2 ≈ 0,87
Х = π/6 = 30° У = 0,5
Х = π/2 = 90° У = 0.


46
Пошаговое объяснение:
Диаметр вписанной окружности в равнобедренной трапеции равен высоте этой трапеции. Соответственно h трапеции = 10 т.к. 2 радиуса.
Зная площадь трапеции можно найти её среднюю линию m = S/h = 115/10 = 11,5. Средняя линия есть сумма оснований трапеции делённая на 2. m = a+b/2. Если в трапецию можно вписать окружность, то сумма оснований такой трапеции = сумме боковых сторон. То есть в нашем случае c+d=a+b=m*2. Периметр трапеции = сумме всех сторон, P = a+b+c+d = m*2 + m*2 = 11,5 *4 = 46