Привет! Вот ответ на твой вопрос .
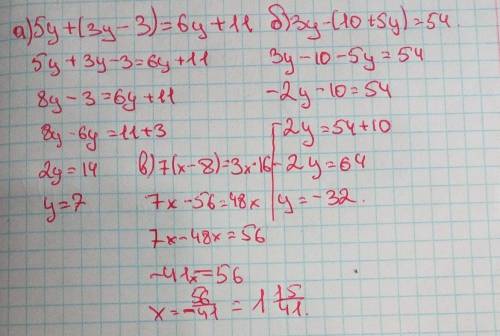
Код обмена информацией-7) 7-битная, кодировка символов, включающая латинский и кириллический алфавит. Производная от кодировки ASCII, заменой латинских букв на кириллические по фонетическому признаку. Характерной особенностью является отсутствие буквы «Ё» (йо) и заглавной буквы «Ъ» (твёрдый знак), однако обнаруживается вариант где эти буквы присутствуют с кодами: 34 (22h) — «Ъ», 35 (23h) — «ё» строчная, 36 (24h) — «Ё» заглавная.
Кодировка может в себя несколько наборов символов:
C0 — основной набор управляющих символов.
C1 — набор дополнительных управляющих символов.
G0 — основной набор графических символов.
G1...G3 — дополнительные наборы графических символов.
Кодировка включает две ссылочных кодовых таблицы, международной (КОИ-7Н0), полностью соответствующей ASCII и представляющих основной набор управляющих символов C0 и графических символов G0, и дополнительной кириллической, (КОИ-7Н1). Кодовые таблицы переключаются управляющими символами 0Fh:ВХ и OEh:ВЫХ:
по коду 0Fh:ВХ включается дополнительная кодовая таблица.
по коду 0Eh:ВЫХ происходит возврат к основной.
На практике работать с неравенствами позволяет ряд свойств числовых неравенств. Они вытекают из введенного нами понятия неравенства. По отношению к числам это понятие задается следующим утверждением, которое можно считать определением отношений «меньше» и «больше» на множестве чисел (его часто называют разностным определением неравенства):
число a больше числа b тогда и только тогда, когда разность a−b является положительным числом;
число a меньше числа b тогда и только тогда, когда разность a−b – отрицательное число;
число a равно числу b тогда и только тогда, когда разность a−b равна нулю.
Это определение можно переделать в определение отношений «меньше или равно» и «больше или равно». Вот его формулировка:
число a больше или равно числу b тогда и только тогда, когда a−b – неотрицательное число;
число a меньше или равно числу b тогда и только тогда, когда a−b – неположительное число.
Основные свойства
Свойство антирефлексивности, выражающееся в том, что для любого числа a неравенства a<a и a>a – неверные.
Действительно, известно, что для любого числа a выполняется равенство a−a=0, откуда в силу разностного определения равных чисел следует равенство a=a. Следовательно, a<a и a>a – неверные неравенства.
Например, 3<3 и - неверные неравенства.
если a>b, то b<a.
Обоснуем его, обратившись к данному выше определению отношений «больше» и «меньше». Начнем с первой части. Так как a<b, то a−b – отрицательное число. При этом b−a=−(a−b) – положительное число, как число, противоположное отрицательному числу a−b. Следовательно, b>a. Аналогично доказывается и вторая часть рассматриваемого свойства.
Свойство транзитивности: если числа a, b и c таковы, что a<b и b<c, то a<c, и если a>b и b>c, то a>c.
Докажем его первое утверждение. Условия a<b и b<c означают, что a−b и b−c – отрицательные числа. Разность a−c можно представить как (a−b)+(b−c), а это есть отрицательное число как сумма двух отрицательных чисел a−b и b−c, что следует из правила сложения отрицательных чисел. Таким образом, a−c – отрицательное число, откуда следует, что a<c, что и требовалось доказать. Абсолютно аналогично доказывается и вторая часть свойства транзитивности.
Пошаговое объяснение:
Смотри решение на фото