4881,85 км
Пошаговое объяснение:
l=2πR; 2R=D, подставим в первую формулу, получим l=πD, тогда D=l/π=15329 км/3,14=4881,85 км
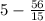
5 - это
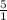
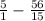
Сначала нужно найти общий знаменатель (найти наименьшее общее кратное 1 и 15 (сейчас это 15)), затем, разделить каждый общий знаменатель на знаменатели дробей и не это число умножить числитель. (общий знаменатель - 15. заменитель первой дроби - 1. 15 ÷ 1 = 15. это значит, что числитель первой дроби нужно умножить на 15). тоже самое делаем с второй дробью. (Я записываю дополнительный множитель в скобках вплотную к числу).
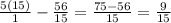
Затем, домножив числители выполняем действие (В знаменателе у нас общий знаменатель).
Сокращаем: просто ищем число, на которое можно одновременно разделить оба числа, чтобы получить другие целые числа. (сейчас я выбрал 3)
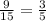
Теперь будет проще перевести дробь в десятичную. Дробь - это деление числителя на знаменатель, поэтому её можно записать, как:
3 ÷ 5 = 0.6
ответ: 0.6
интеграл расходится
Пошаговое объяснение:
решим сначала данный интеграл как несобственный(без пределов), а потом подставим пределы:
1) *интеграл *(3х²dx)/(x³+1)=...
используем подстановку для упрощения интеграла:
t=х³+1
dt=(x³+1)' *dx=3x² *dx
получаем: ...=*интеграл* (1/t)dt=...
вычисляем: ...=ln |t|=...
выполняем обратную замену: ...=ln |x³+1|=...
прибавляем константу интегрирования С (СєR): ...=ln |x³+1|+C
2) подставляем пределы:
тогда *интеграл от 0 до ∞*(3х²dx)/(x³+1)=
=lim (ln |x³+1|)-lim (ln |x³+1|)=
x—›∞. x—›0
=lim (ln |+∞|)-lim (ln |1|)=+∞-0=+∞ —›
x—›∞. x—›0
интеграл расходится
Из формулы длины окружности:
L = 2πR = πD, где:
L - длина окружности;
R, D - соответственно радиус и диаметр окружности;
π = 3,14...;
имеем:
D = L/π = 15329/3,14 = 4881,85 км. ≈ 4882 км.