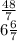
S1=70; S1=a*b, a=70/b. S2=70; S2=(a-4)(b+2). Составим уравнение: (70/b-4)(b+2)=70. Решим уравнение относительно b. (70-4b)(b+2)=70b; 70b +140-4b^2-8b=70b; -4b^2-8b+140=0;
-b^2-2b+35=0; b^2+2b-35=0; D= 2^2-4*(-35)=144; b1=(-2-12)/2=-14/2=-7 (не подходит, т.к. <0). b2=(-2+12)/2=10/2=5 (м)- ширина одного прямоугольника; a=70/5=14 (м) – длина одного прямоугольника. Следовательно, 14-4=10 (м) – длина другого прямоугольника, 5+2=7 (м)- ширина пдругого прямоугольника. ответ: стороны прямоугольников – 7м и 10м, 5м и 14м. Как то так.натуральное число - это целое и положительное, минимальное натуральное число это 1
пусть искомое число Х, тогда х / (3/25) = 25х/3, то есть нужно такое число х которое при умножении на 25 делилось бы нацело на 3. 25 на 3 не делится, тогда х должен делится нацело на 3, чтобы дробь сократилась. Минимальное натуральное число кратное 3 это и есть 3.
Аналогично втоорой случай х / (9/10) = 10х/9
Минимальное натурально число кратное 9 это и есть 9.
Если брать одно число которое подходило бы к обоим случаем тогда это будет 9