Примем величину всего заказа за 1.
пусть х дней требуется первому, у дней - второму. тогда 1/х - производительность первого, 1/у - производительность второго. За 6 дней совместной работы сделано 6(1/х+1/у), а 10 дней второй сделал 10/у. Получим систему
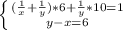
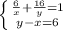
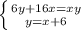
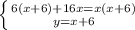
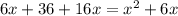
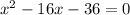
x=18 или х=-2-не удовл. условию.
Значит, 18 дней требуется первому, 18+6=24 дня - второму.
ответ: 18 и 2 дня.
Відповідь:
14 часов
Покрокове пояснення:
Для решения задачи сперва нужно определить количество времени за которое бассейн наполняется через 2 трубы.
Для этого находим продуктивность работы каждой из труб за 1 час.
Поскольку вся работа равна 1, получим.
1/12 продуктивность работы первой трубы за час.
1/24 продуктивность работы второй трубы за час.
1/12+1/24=3/4=1/8. Продуктивность работы двух труб за час вместе.
Находим количество работы для второй трубы за 9 часов.
Получим.
1/24*9=3/8.
Находим количество работы выполненное первой трубой.
1-3/8=5/8.
Находим период работы двух труб вместе.
5/8 / 1/8=5/8*8/1=40/8=5 часов.
Находим период наполнения.
5+9=14 часов.
Примем всю работу за 1
х (дней) - выполнял всю работу первый рабочий
х+10 (дней) - выполнял всю работу второй рабочий
1/6 - общая производительность двух рабочих, составим ур-е
1/х+1/(х+10)=1/6
(х+10+х)/(х^2+10х) = 1/6
х^2 + 10х = 6*(2х+10)
х^2+10х=12х+60
х^2+10х-12х-60=0
х^2-2х-60=0
D= ...(дискриминант)
х= (дней) - понадобится первому рабочему
...+10=... (дней) - понадобится второму рабочему
Проверка
1/...+1/30
ответ: за ...дней выполнит работу первый рабочий, за ... дней - второй