1) (0,6х-5,1)/0,27=3,4
0,6х-5,1=0.918
0.6x=6,018
x=10,03
2) пуст второе число х, тогда первое 2,5+х. Известно, что среднее арифметическое этих чисел 5,75 или 2х+2,5/2.
Составлю и решу уравнение
2х+2,5/2=5,75
2х+2,5=11,5
2х=9
х=4,5 - второе число
2,5+4,5=7 первое число
1. область определения любое значение хЄR
область значений yЄR( чаще всего об этом можно говорить после построения графика)
2.y(-x)=-2x^3-9x^2-12x-5 функция не является четной или нечетной
3.не периодическая
4. точки пересечения с осями координат
ОХ у=0 х=1, 2x^3-9x^2+12x-5=(x-1)(2x^2-7x+5)=0
2x^2-7x+5=0, D=9, x=2,5 и х=1
(1;0),(2,5;0)
OY x=0, y=-5 (0;-5)
5. Находим производную, она равна 6x^2-18x+12
Находим точки экстремума и промежутки возрастания и убывания
6x^2-18x+12=0
x^2-3x+2=0
D=1
x1=2, x2=1
Наносим данные значения на коорд. прямую и определяем знак производной
+ - +
X max=1
x min=2
xЄ -бесконечности до 1 и от 2 до + бесконечности функция возрастает
хЄ от 1 до 2 убывает
упрощаем выражение, получаем y=x^3-25*x^2-208*x-586, возьмем первую производную от данного выражения:
y'=3x^2-50x-208, исследуем поведение функции, найдем нули производной получаем 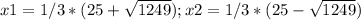
Это парабола, ветви направлены ввех, т.к коэффициент перед х^2>0, значит она меньше нуля на промежутке (х2;х1)
Промежуток (2.8;5) включен в промежуток (х2;х1), значит на нем функция y=x^3-25*x^2-208*x-586 убывает, т.к производная <0. Если функция убывает то наибольшее значение функции будет достигаться на границе промежутка.
Т.к. в задаче речь идет о промежутке, а не об отрезке, то нельзя найти строгое решение задачи, только предел.
Будем предполагать что речь идет об отрезке [2.8;5].
Подставим х=2.8 в исходное выражение и получим -177. 648
ответ: наибольшее значение достигается при х=2.8 и равно -177.648
P.S. я указал только метод решения, сами вычисления лучше проверить.
х=10,03
2) Пусть х-второе число,тогда х+2,5-первое:
2х=5,75*2-2,6=9
х=4,5
Следовательно первое 4,5+2,5=7