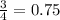
Пошаговое объяснение:
В принципе, решение можно осуществить 2 путями. Для начала, обозначим вероятности
Pн - нечетное произведение очков,
Рч - четное произведение очков
1. При двух бросках в результате могут быть только 2 вероятных события:
- четное произведение очков
- нечетное произведение очков.
Эти 2 случая охватывают полностью возможные наступления событий.
Соответственно, верно равенство
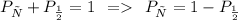
Произведение 2 чисел будет НЕчетным тогда, когда НЕчетными являются ОДНОВРЕМЕННО ОБА из множителей.
Два броска являются независимыми (результат 2 броска не зависит от числа, выпавшего первым);
Из равновероятных 6 событий для одного броска нечетныеэми будут 3.
Следовательно, вероятность нечетного броска равна 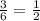
Вероятность того, что произведение чисел бросков будет нечетным равна вероятности двойного нечетного броска - т.е. произведению вероятностей для 1 и 2 броска:
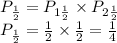
Следовательно, вероятность того, что произведение чисел бросков будет четным равна разности между 1 и Рн:
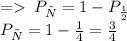
2. Возможны варианты бросков (первый-второй броски):
1 - чч - четный-четный
2 - чн - четный-нечетный
3 - нч - нечетный-четный
4 - нн - нечетный-нечетный.
Произведение же четно, когда четным является ХОТЯ БЫ ОДИН из множителей.
А это происходит в трех случаях из 4-х - случае 1, 2 и 3 из указанных выше.
То есть
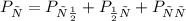
Легко проверить, что вероятность наступления каждого из событий равна:
произведению вероятности четности/нечетности первого броска на вероятность четности/нечетности второго броска.
Для любого броска вероятность четного числа очков равна вероятности нечетного и составляет 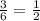
Следовательно:
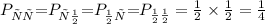
А значит,
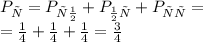
Итак, в двух различных решениях получили одинаковые результаты. Следовательно, ответ верен:
ответ : 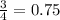
Проце́нт — одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому. Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть 85 кг.
Правила набора
В тексте знак процента используется только при числах в цифровой форме, от которых при наборе отделяется неразрывным пробелом (доход 67 %), кроме случаев, когда знак процента используется для сокращённой записи сложных слов, образованных при числительного и прилагательного процентный. Например: 20%-я сметана (означает двадцатипроцентная сметана), 10%-й раствор, 20%-му раствору, но жирность сметаны составляет 20 %, раствор концентрацией 10 % и т. п.
Это правило набора введено в действие в 1982 году нормативным документом ГОСТ 8.417—81 (впоследствии заменённым на ГОСТ 8.417—2002); ранее нормой было не отделять знак процента пробелом от предшествующей цифры. В настоящее время правило отбивки знака процента не является общепризнанным. До сих пор многие российские издательства не следуют рекомендациям ГОСТ 8.417—2002 и по-прежнему придерживаются традиционных правил набора, то есть при наборе знак процента от предшествующего числа не отделяется.
Разговорное употребление
«Работать за проценты» — работать за вознаграждение, исчисляемое в зависимости от прибыли или оборота.«На все сто (процентов)» — прекрасный во всех отношениях; всецело, полностью, целиком[1].«Процентщик» — человек, ссужающий деньги под большие проценты, ростовщик.
Сравнение величин в процентах
Иногда бывает удобным сравнивать две величины не по разности их значений, а в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах. Если сравнение по разности вполне однозначно, то есть всегда можно найти, насколько одна величина больше или меньше другой, то для сравнения в процентах нужно указывать, относительно какой величины вычисляется процент. Такое указание, впрочем, необязательно в том случае, когда говорят, что одна величина больше другой на число процентов, превышающее 100. В этом случае остается только одна возможность вычисления процента, а именно деление разности на меньшее из двух чисел с последующим умножением результата на 100.
Процент – это сотая часть единицы. Запись 1% означает 0.01. Существует три основных типа задач на проценты:
Задача 1. Найти указанный процент от заданного числа. Заданное число умножается на указанное число процентов, а затем произведение делится на 100.
П р и м е р . Вклад в банке имеет годовой прирост 6%. Начальная сумма вклада равнялась 10000 руб. На сколько возрастёт сумма вклада в конце года? Р е ш е н и е : 10000 · 6 : 100 = 600 руб.
Задача 2. Найти число по заданному другому числу и его величине в процентах от искомого числа. Заданное число делится на его процентное выражение и результат умножается на 100.
П р и м е р . Зарплата в январе равнялась 1500 руб., что составило 7.5% от годовой зарплаты. Какова была годовая зарплата?
Р е ш е н и е : 1500 : 7.5 · 100 = 20000 руб.
Задача 3. Найти процентное выражение одного числа от другого.Первое число делится на второе и результат умножается на 100.П р и м е р . Завод произвёл за год 40000 автомобилей, а в следующем году – только 36000 автомобилей. Сколько процентов это составило по отношению к выпуску предыдущего года?
Р е ш е н и е : 36000 : 40000 · 100 = 90% .
Пошаговое объяснение:
тут на 2 страницы