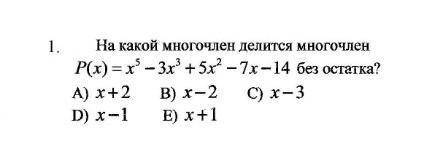
1) Начнём ставить ладьи по очереди. Для ладьи в первой строке есть 8 вариантов расстановки. Для ладьи во второй строке 7 (кроме того столбца, в котором стоит первая ладья), для ладьи из третьей - 6 и т.д
По правилу произведения получим 8×7×6×1=8!=40320 возможных расстановок.
2) На первом любая из 5 цифр может стоять, 5 вариантов.
На втором любая из оставшихся 4, 4 варианта.
На третьем любая из оставшихся 3, 3 варианта.
На 4-ом любая из оставшихся 2, 2 варинта.
На 5-ом только последняя неиспользованная.
5×4×3×2×1=120.
3) 6×5×4×3×2×1=720
4) У нас 7 человек в команде.
Сначала выберем капитана. Это можно сделать 7-ю
Выбираем вратаря. Осталось 6 человек (т.к капитан уже занят). Значит
Чтобы итоговое кол-во умножим полученные 6×7=42. ответ:42
5) комбираторика.
6) 5!/(5-3)!=5×4×3×2×1/2=20×3=60 (разных трёхцветных трёхполосных флагов)
7) …
8) Попробую предположить: Число
Когда Иванов попадет 50!/(4!*(50-4)!)-49!/(4!*(49-4)!)=18424
9) …
10) …
Задание 1
Сотая доля числа, принимаемого за целое (обозначается знаком %)
Задание 2
Чтобы перевести проценты в дробь, нужно убрать знак «%» и разделить число на 100. Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак «%». Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.
40%=40/100=4/10=2/5
37%=37/100
20%=20/100=2/10=1/5
12,5%=125/1000=1/8
Задание 3
Чтобы перевести проценты в десятичную дробь нужно: разделить число процентов на 100 и убрать знак процента "%" или перенести запятую на две цифры влево.
40%= 40:100=0,4
37%=37:100=0,37
20%=20:100=0,2
12,5=12,5:100=0,125
Задание 4
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак «%». Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.
1/2=1/2*5/5=5/10=0,5*100=50%
3/5=3/5*2/2=0,6*100=60%
0,27*100=27%
0,04*100=4%
Задание 5
4000:100=40(кг)-1%
40*23%=920(кг)-23%
ответ: 920 кг
Задание 6
6:25*100=24
6:25=0,24
0,24*100=24
ответ: Полное число 24
B) x – 2
Пошаговое объяснение:
x = 2 является корнем уравнения x⁵ – 3x³ + 5x² – 7x – 14 = 0:
2⁵ – 3·2³ + 5·2² – 7·2 – 14 = 32 – 24 + 20 – 14 – 14 = 0
Следовательно, многочлен P(x) можно представить в виде P(x) = (x – 2)·P'(x) -- делится без остатка на (x – 2).