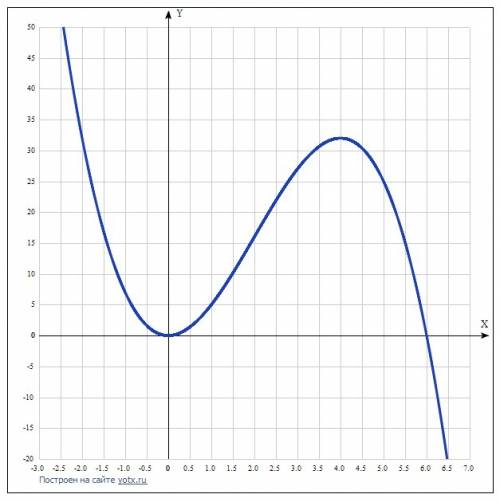
Область определения функции. ОДЗ:-∞<x<∞
Точка пересечения графика функции с осью координат Y:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в =-x³+6x².
Результат: y=0. Точка: (0, 0)
Точки пересечения графика функции с осью координат X:
График функции пересекает ось X при y=0, значит, нам надо решить уравнение:
-x³+6x²= 0
Решаем это уравнение и его корни будут точками пересечения с X:
-x3+6x² = -x²(х-6) = 0
x=0. Точка: (0, 0)
x=6. Точка: (6, 0) .
Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y'=-3x² + 12х=0
Решаем это уравнение и его корни будут экстремумами:
-3x² + 6х = -3x(х-4) = 0.
x=0. Точка: (0, 0)
x=2. Точка: (4, 32)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимум функции в точке: x_{2} = 0.
Максимум функции в точках: x_{2} = 4.
Возрастает на промежутке [0, 4].
Убывает на промежутках (-oo, 0] U [4, oo).
Для того, чтобы найти значение переменно y, при которой 25y больше 7y на 414. Чтобы ответить на вопрос задачи составим и решим линейное уравнение с одной переменной.
25y - 7y = 414.
Решать уравнение будем с тождественных преобразований.
Приведем подобные слагаемые в левой части уравнения и получим уравнение:
y(25 - 7) = 414;
18y = 414;
Искать значение переменной y будем как неизвестный множитель, разделив произведение на известный множитель.
y = 414 : 18;
y = 23.
ответ: при y = 23 выполняется условие задачи.
Пошаговое объяснение:
Пошаговое объяснение:
-3х-75=-10
-3х=-10+75
-3х=65
х=65:(-3)