1) 10
2) 28
3) 13
Пошаговое объяснение:
1) Пусть числитель состоит из суммы квадратов следующих пяти последовательных натуральных чисел:
n, n+1, n+2, n+3, n+4.
По условию сумма трех меньших квадратов равна сумме двух наибольших квадратов, то есть
n² + (n+1)² + (n+2)² = (n+3)² + (n+4)².
Раскроем скобки и упростим уравнение:
n² + n² + 2·n + 1 + n² + 4·n + 4 = n² + 6·n + 9 + n² + 8·n + 16
n² - 8·n - 20 = 0
Решаем последнее квадратное уравнение
D=(-8)² - 4 · 1 · (-20) = 64 + 80 = 144 = 12²
n₁ = (8 - 12)/(2·1) = -4/2 = -2 - не является натуральным числом, отпадает.
n₂ = (8 + 12)/(2·1) = 20/2 = 10
Значит, первое из пяти чисел - это 10. Определим сумму в числителе:
10² + (10+1)² + (10+2)² + (10+3)² + (10+4)² = 100 + 121 + 144 + 169 + 196 = 730.
Тогда значение дроби равно
730 / 73 = 10
2) Так как 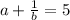 и
и 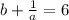 , то
, то
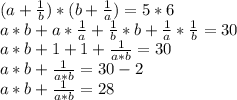
3) Утверждение "Всякое число, не делящееся на 26, не делится на 13" ложно, если число имеет вид 26·m+13, где m=0, 1, 2, ... (числа, кратные на 13, но не кратные на 26). Тогда, отрицание этого утверждения "Не всякое число, не делящееся на 26, не делится на 13" истинно для чисел имеющих вид 26·m+13. Наименьшее из них - это 13.
8×8-6×6=8*8=64 6*6=36 63-36=28
4×6+2×8= 4*6=24 2*8=16 24+16=40
32:4+7×8=32/4=8 7*8=56 56+8=64
8×(24-18)= 24-18=6 6*8=48
64:(40-32)=40-32=8 64/8=8(70-65)×6=70-65=5 5*6=30
37+7×6=37+7=44 44+6=50
60-24:6×8=24/6=4 4*8= 32 60-32=28
32+7×9-16=32+ 7*9=63 63+32=95 95-16=79
9×3-64:8=9*3=27 64/8=8 27-8=19
8×(11-5)+52=11-5=6 6*8=48 48+52=100