На обратную дорогу он потратил на 5 минут больше
1 ч. 5 мин. =13/12 ч.
Пусть х км/ч - скорость на подъёме, тогда скорость на спуске - (х+2) км/ч. Пусть у км - расстояние от станции до вершины горы, тогда расстояние от вершины горы до озера - (5-у) км. На дорогу от станции до озера рыболов затратил у/x+(5-y)/(x+2) или 1 час; на обратную дорогу - (5-у)/x + у/(х+2) или 1,1 часа. Составим и решим систему уравнений: (фото)
По теореме Виета корнями уравнения
var > x2 - 2, 8.x - 4, 8 = 0 < /var >
являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.
Путь от станции до вершины (4 2- 3*4)/2=2 км, от вершины до озера 5-2=3 км.
ответ: скорость на подъёме 4 км/ч, скорость на спуске 6 км/ч.


Наверное, всё-таки на обратную дорогу он потратил на 5 минут больше
1 ч. 5 мин.=13/12 ч.
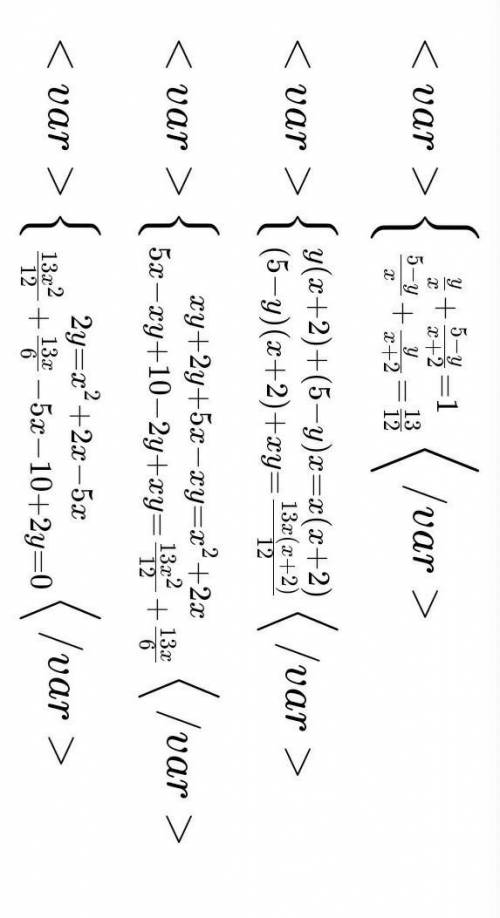
Пусть х км/ч - скорость на подъёме, тогда скорость на спуске - (х+2) км/ч. Пусть у км - расстояние от станции до вершины горы, тогда расстояние от вершины горы до озера - (5-у) км. На дорогу от станции до озера рыболов затратил y/x+(5-y)/(x+2) или 1 час; на обратную дорогу - (5-у)/х + у/(х+2) или 1,1 часа. Составим и решим систему уравнений:
\{ {{\frac{y}{x}+\frac{5-y}{x+2}=1} \atop {\frac{5-y}{x}+\frac{y}{x+2}=\frac{13}{12}}}{x5−y+x+2y=1213xy+x+25−y=1
\{ {{y(x+2)+(5-y)x=x(x+2)} \atop {(5-y)(x+2)+xy=\frac{13x(x+2)}{12}}}{(5−y)(x+2)+xy=1213x(x+2)y(x+2)+(5−y)x=x(x+2)
\{ {{xy+2y+5x-xy=x^2+2x} \atop {5x-xy+10-2y+xy=\frac{13x^2}{12}+\frac{13x}{6}}}{5x−xy+10−2y+xy=1213x2+613xxy+2y+5x−xy=x2+2x
\{ {{2y=x^2+2x-5x} \atop {\frac{13x^2}{12}+\frac{13x}{6}-5x-10+2y=0}}{1213x2+613x−5x−10+2y=02y=x2+2x−5x
\{ {{2y=x^2-3x} \atop {\frac{13x^2}{12}-\frac{17x}{6}-10+2y=0}}{1213x2−617x−10+2y=02y=x2−3x
Произведём подстановку:
\{ {{2y=x^2-3x} \atop {\frac{13x^2}{12}-\frac{17x}{6}-10+x^2-3x=0}}{1213x2−617x−10+x2−3x=02y=x2−3x
\{ {{2y=x^2-3x} \atop {\frac{25x^2}{12}-\frac{35x}{6}-10=0}}{1225x2−635x−10=02y=x2−3x
Домножим второе уравнение на 12/25:
\{ {{2y=x^2-3x} \atop {x^2-2,8x-4,8=0}}{x2−2,8x−4,8=02y=x2−3x
По теореме Виета корнями уравнения x^2-2,8x-4,8=0x2−2,8x−4,8=0 являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.
Путь от станции до вершины (4^2-3*4)/2=2 км, от вершины до озера 5-2=3 км.
ответ: скорость на подъёме 4 км/ч, скорость на спуске 6 км/ч.
В решении.
Пошаговое объяснение:
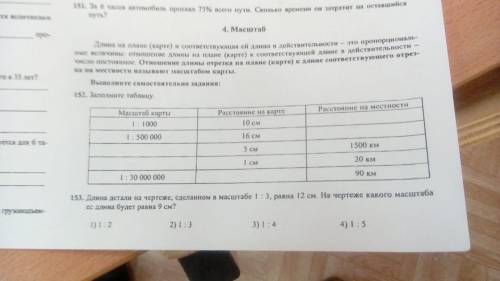
152.
Таблица
Масштаб карты Расстояние на карте Расстояние на местности
1) 1 : 1000 10 см 100 м
Масштаб 1 : 1000 означает, что в 1 см на карте 1000 см на местности.
Перевести в метры: 1000 : 100 =в 1 см на карте 10 м на местности.
10 м * 10 см = 100 м на местности.
2) 1 : 500 000 16 см 80 км
Масштаб 1 : 500 000 означает, что в 1 см на карте 500 000 см на местности.
Перевести в метры: 500 000 : 100 = в 1 см на карте 5 000 м на местности.
Перевести в км: 5 000 : 1000 = в 1 см на карте 5 км на местности.
5 км * 16 = 80 км на местности.
3) 1 : 30 000 000 5 см 1500 км
В 1 см на карте 1500 : 5 = 300 км на местности.
Перевести в см: 300 * 1000 * 100 = 30 000 000 см в 1 см на карте.
Масштаб карты 1 : 30 000 000.
4) 1 : 2 000 000 1 см 20 км
В 1 см на карте 20 км на местности.
Перевести в см: 20 * 1000 * 100 = 2 000 000 см в 1 см на карте.
Масштаб карты 1 : 2 000 000.
5) 1 : 30 000 000 0,3 см (30 мм) 90 км
Масштаб 1 : 30 000 000 означает, что в 1 см на карте 30 000 000 см на местности.
Перевести в метры: 30 000 000 : 100 = в 1 см на карте 300 000 м на местности.
Перевести в км: 300 000 : 1000 = в 1 см на карте 300 км на местности.
90 : 300 = 0,3 см на карте, или 30 мм.
153.
При масштабе 1 : 3 деталь, длина которой на чертеже 12 см, в действительности длиной 36 см (12 * 3 = 36 см).
Соответственно, если на чертеже длина детали будет 9 см, масштаб будет 1 : 4 (36 : 9 = 4).