Числа A и B называются взаимно простыми, если НОД(А; В)=1.
Возможны различные варианты :
а) Если числа А и В простые, то НОД(А; В)=1. Например:
НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.
1) 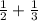
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6
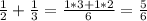
2) 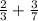
НОД(3; 7)=1, то НОК(3; 7)=3·7=21
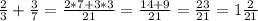
б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:
НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.
3) 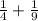
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36
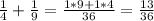
2) 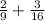
НОД(9; 16)=1, то НОК(9; 16)=9·16=144
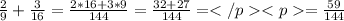
В общем случае, если А и В взаимно простые, то есть
НОД(А; В)=1, то НОК(А; В)=А·В.
х -скорость 1
у -скорость 2
t -время встречи 1 и 2
xt-yt=20
yt=10x ⇒t=10x/y, подставляем в 1 и 3 ур-е
xt+9x=9y
(10x/y)(х-у)=20 ⇒х²-ху-2у=0 ⇒у=х²/(х-2)
10x²/y=9у-9х ⇒9у²-9ху-10х²=0
9у²-9ху-10х²=0 решаем относительно у
д=(9х)²+9*4*10х²=441х²=(21х)²
у=(9х±21х)/18=30х/18; -12х/18 подставляем у
30х/18=5х/3=х²/(х-2)
3х²=5х²-10х
2х²=10х
х(х-5)=0 ⇒х=5; 0
-12х/18=-2х/3=х²/(х-2)
-2х²+4х=3х²
5х²-4х=0
х(х-4/5)=0
х=0,8; 0 у=х²/(х-2) ⇒у=0,64/(-1,2) нет решения
ответ: скорость первого 5 км/ч