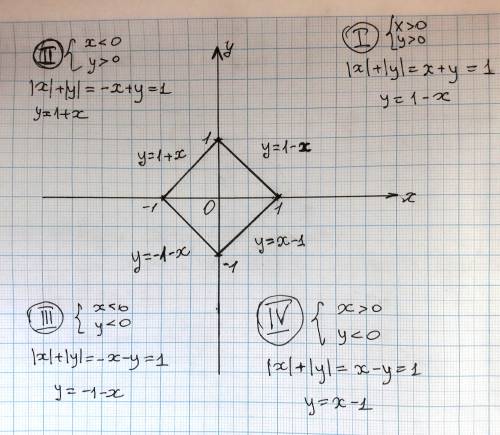
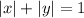воспользуемся определением модуля числа: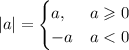
и 
остаётся постоянным, поэтому в каждом квадранте можно избавиться от модулей и построить соответствующие фрагменты графика .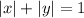
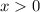и 
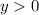, тогда 
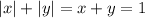, поэтому в I-й четверти строим график функци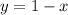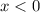и 
.
и 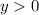, тогда 
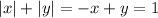, поэтому во II-й четверти строим график функци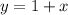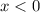и 
. и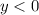 
, тогда 
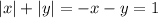, поэтому в III-й четверти строим график функци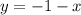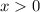и 
. и 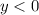, тогда 
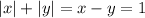, поэтому в IV-й четверти строим график функции 
.
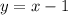б)
4 * (2 1/4 - 1 7/8 ) = 4 * ( 9/4 - 15/8 ) =
=4/1 * 9/4 - 4/1 * 15/8 =
= 9 - 15/2 = 9 - 7 1/2 = 1 1/2
по действиям:
1) 2 1/4 - 1 7/8 = 9/4 - 15/8 = (18-15)/8 = 3/8
2) 4 * 3/8 = (4*3)/(1*8) = 3/2 = 1 1/2
в)
4 1/4 * 4/9 + 4/9 * 1 1/2 =
=4/9 * (4 1/4 + 1 1/2) =
= 4/9 * ( 4 1/4 + 1 2/4) =
= 4/9 * 5 3/4 = 4/9 * 23/4=
=23/9 = 2 5/9
по действиям:
1) 4 1/4 * 4/9 = 17/4 * 4/9 = 17/9 = 1 8/9
2) 4/9 * 1 1/2 = 4/9 * 3/2 = (2*1)/(3*1) = 2/3
3) 1 8/9 + 2/3 = 17/9 + 6/9 = 23/9 = 2 5/9