1)
2(3x + 1) - x ≤ 3(x + 4)
6х + 2 - х ≤ 3х+12
5х + 2 ≤ 3х + 12
5х - 3х ≤ 12 -2
2х ≤ 10
х ≤5,
2)
7x + 4(x - 2) > 6(1 + 3x)
7х + 4х - 8 > 6 + 18x
11x - 8 > 6 + 18x
11x - 18x > 6 + 8
-7x > 14
x < - 2
3)
2(x - 1) - 3(x + 2) < 6(1 + x)
2x - 2 - 3x - 6 < 6 + 6x
-x - 8 < 6 + 6x
-x - 6x < 6 + 8
-7x < 14
x > -2
4)
7(y + 3) - 2(y + 2) ≥ 2(5y + 1)
7y + 21 - 2y - 4 ≥ 10y + 2
5y + 17 ≥ 10y + 2
5y - 10y ≥ 2 - 17
-5y ≥ -15
y ≤ 3
Пошаговое объяснение:
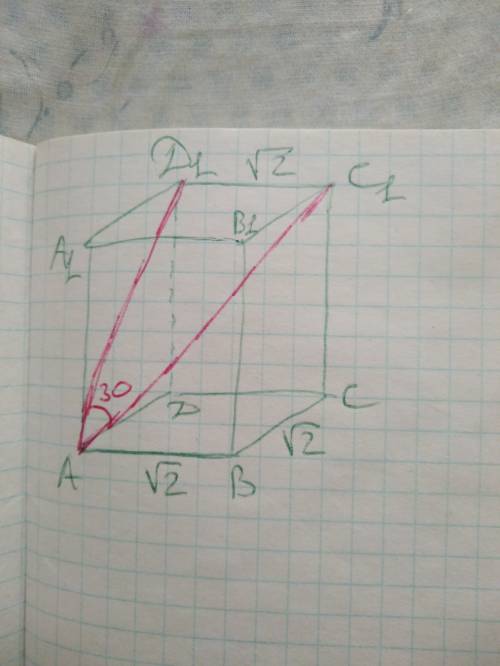
4 куб.см.
Пошаговое объяснение:
Вот рисунок. AB = BC = C1D1 = √2; AC = √2*√2 = 2
Угол между диагональю призмы AC1 и боковой плоскостью ADD1A1 - это на самом деле угол между диагональю призмы AC1 и диагональю грани AD1.
В треугольнике AC1D1 углы 90°, 30° и 60°.
Гипотенуза вдвое больше катета против угла 30 гр.
AC1 = 2*C1D1 = 2√2.
Теперь рассмотрим прямоугольный треугольник ACC1.
Высоту призмы CC1 найдем из теоремы Пифагора:
CC1^2 = AC1^2 - AC^2 = (2√2)^2 - 2^2 = 8 - 4 = 4
CC1 = √4 = 2
Объем призмы равен
V = AB*BC*CC1 = √2*√2*2 = 4 куб.см.
х-100%
х/1.25 - у%
ху=100х/1.25
ху=80х
у=80 % стало
100-80=20 на 20 % уменьшилась площадь