Находим значение следующего выражения: 6x*0,3+4*(1,3x+20y) при x=1, y=0,1. Для того чтобы решить данный пример подставляем известные значения х и в в данное выражение. Записываем решение.
6x*0,3+4*(1,3x+20y) при x=1, y=0,1.
6 х × 0,3 + 4 × (1,3 х + 20у) = 6 × 1 × 0,3 + 4 × (1,3 × 1 + 20 × 0,1) = 6 × 0,3 + 4 × (1,3 + 2) =
= 1,8 + 4 × 3,3 = 1,8 + 13,2 = 15.
То есть при решении данного примера получается ответ равный 15.
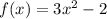
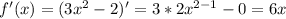
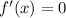
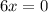
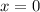
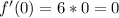
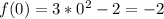
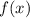монотонно убывает на интервале знакопостоянства производной: x∈(-∞;0) 
Пошаговое объяснение:1) f(x)= 2x²-3x+1 , [-1;1] ⇒ f'(x)= 4x-3, найдём критические точки: 4х-3=0, ⇒ х = 3/4=0,75 ∈[-1;1]. Найдём значения функции в критической точке и на концах данного промежутка: f(3/4)= 2·(3/4)²- 3·3/4 +1 =9/8 -9/4 + 1 = -1/8 ; f(1) = 0; f(-1)=6 ⇒ max f(x)=f(-1)=6; minf(x)=f(3/4)=-1/8
2)f(x)=3x²-4 на [2;4] ⇒ f'(x)=6x 6x=0, x=0-крит. точка, но x=0∉ [2;4] ⇒ Найдём значения функции на концах данного промежутка: f(2)= 3·2²-4= 12-4=8 f(4)=3·4² - 4= 48-4=44 ⇒ max f(x)=f(-4)=44; minf(x)=f(2)=8 3)f(x)=x²-1 на [0;3]⇒ f'(x)=2x , 2x=0 x=0 -критическая точка х=0 ∈ [0;3]. Найдём значения функции в критической точке и на концах данного промежутка: f(0) =0²-1=-1; f(3)=3²-1=8 ⇒max f(x)=f(3)=8; minf(x)=f(0)= -1
6х*0.3+4*(1.3х+20у) = 1,8х+5.2х+80у = 7х=80у = 7*1 + 80*0.1 = 7+8=15
Пошаговое объяснение: