Пошаговое объяснение:
ДАНО:Y(x) = x³ -6*x² +4.
ИССЛЕДОВАНИЕ.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Вертикальная асимптота - нет - нет разрывов.
3. Наклонная асимптота - y = k*x+b.
k = lim(+∞) Y(x)/x = +∞ - нет наклонной (горизонтальной) асимптоты.
4. Периода - нет - не тригонометрическая функция.
5. Пересечение с осью OХ.
Применим тригонометрическую формулу Виета.
Разложим многочлен на множители. Y=(x+0,77)*(x-0,88)*(x-5,88)
Нули функции: Х₁ =-0,77, Х₂ =0,88, Х₃ =5,88
(без комментариев, без расчёта).
6. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;-0,77]U[0,88;5,88]
Положительная -Y(x)>0 X∈[-0,77;0,88]U[5,88;+∞)
7. Пересечение с осью OY. Y(0) = 4
8. Исследование на чётность.
В полиноме есть и чётные и нечётные степени - функция общего вида.
Y(-x) ≠ Y(x). Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
9. Первая производная. Y'(x) = 3*x² -12*x = 3*x*(x-4) = 0
Корни Y'(x)=0. Х₄ =0 Х₅=4
Где производная отрицательна (между корнями), там функция убывает.
10. Локальные экстремумы.
Максимум - Ymax(X₄= 0) =4. Минимум - Ymin(X₅ = 4) =-28
11. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;0;]U[4;+∞) , убывает - Х∈[0;4] (между корнями).
ВАЖНО! Функция непрерывная - скобки квадратные.
12. Вторая производная - Y"(x) = 6* x -12 = 6*(х-2) = 0
Корень второй производной - точка перегиба Х₆=2
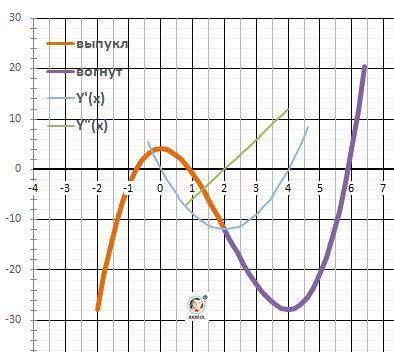
13. Выпуклая “горка» Х∈(-∞; Х₆ = 2] - производная Y"(x)<0 - отрицательная)
Вогнутая – «ложка» Х∈[Х₆ = 2; +∞).
14. График в приложении. Дополнительно схема/шаблон для анализа функции.

26
Пошаговое объяснение:
обозначим Р₁-рубашки в мамином шкафу, Б₁-брюки в мамином шкафу
Р₂-рубашки в папином шкафу, Б₂-брюки в папином шкафу
Р₁/Б₁=2/3 Р₁=2Б₁/3 Р₂/Б₂=3/4 Р₂=3Б₂/4
2Б₁/3+3Б₂/4=19 |·12
8Б₁+9Б₂=228
8Б₁=228-9Б₂ левая часть равенства делится на 8, значит, на 8 должна делиться и правая часть
пусть Б₂=8k k∈Z 228-9·8k=228-72k не делится на 8
Б₂=8k+1 228-9(8k+1)=219-72k не делится на 8
Б₂=8k+2 228-9(8k+2)=210-72k не делится на 8
Б₂=8k+3 228-9(8k+3)=201-72k не делится на 8
Б₂=8k+4 228-9(8k+4)=192-72k делится на 8
Б₂=8k+5 228-9(8k+5)=183-72k не делится на 8
Б₂=8k+6 228-9(8k+6)=174-72k не делится на 8
Б₂=8k+7 228-9(8k+7)=165-72k не делится на 8
значит, Б₂=8k+4 8Б₁=192-72k 8Б₁=8(24-9k) Б₁=24-9k
т.к. значение Б₁ должно быть положительным 24>9k k=0,1,2
k=0 Б₁=24-9·0=24 Б₂=8·0+4=4 Б₁+Б₂=24+4=28
k=1 Б₁=24-9=15 Б₂=8+4=12 Б₁+Б₂=15+12=27
k=2 Б₁=24-18=6 Б₂=16+4=20 Б₁+Б₂=6+20=26
BC = 78.75/3.5 = 22.5
AB = BC + AC =101.25