x ∈ (1; 2] ∪ {3}
Пошаговое объяснение:
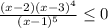
решим неравенство методом интервалов. Для этого приравняем и числитель и знаменатель к нулю:
x-2=0; x=2
x-3=0; x=3
x-1=0; x=1
изобразим точки на координатной прямой. Точка "1" будет выколота, так как она обнулит знаменатель, а на 0 делить нельзя. Точки "2" и "3" будут закрашенными, т.к знак неравенства "меньше или равно" (см рис)
знак крайнего правого интервала будет + (можно взять число "100" и подставить в неравенство), дальше "+"; "-"; "+" (подставляем точки из этих интервалов в неравенство и ищем знак)
т.к знак неравенства "≤0", то выбираем интервалы с "-"
также отдельно берем точку "3", т.к она обнулит числитель, а это нас устраивает
x ∈ (1; 2] ∪ {3}
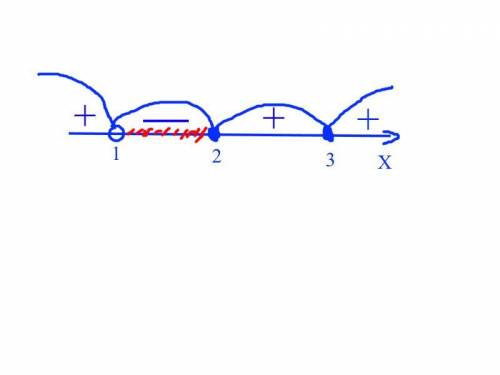
16
Пошаговое объяснение:
Логично предположить, что 128 фуксиков можно сложить из самых маленьких манет А.
Значит 128 делится на А
Подберём числа:
128:1=128
128:128=1
128:2=64
128:64=2
128:8=16
128:16=8
128:4=32
128:32=4
128 -не подходит (т.к. из чисел 128,129,130 нельзя получить 131)
1 - не подходит (т.к. из чисел 1,2,3 можно получить 127)
64 - не подходит (т.к. из чисел 64,65,66 нельзя получить 139)
2 -не подходить (т.к. из чисел 2,3,4 можно получить 127)
8 - не подходит (т.к из чисел 8,9,10 можно получить 127)
32 - не подходит ( т.к. из чисел 32,33,34 нельзя сделать 137)
4 - не подходит (т.к. из чисел 4,5,6 можно сделать 127)
Методом подбора установили, что А=16
А+1=16+1=17
А+2=16+2=18
Проверка:
16*7=112 (127-112=15 не хватает), если заменить все числа 16 на 18, то получим
18*7=126 (не хватает 1)
Вывод: Из чисел 16,17,18 нельзя получить число 127
128 = 16*8
129=16*7+17
130=16*7+18
131=16*6+17+18
132=16*6+18+18
133=16*5+17+2*18
134=16*5+3*18
135=16*4+17+3*18
136=16*4+4*18
137=16*3+17+4*18
138=16*3+5*18
139=16*2+17+5*18
140=16*2+6*18
141=16+17+6*18
142=16+7*18
143=17+7*18
144=8*18
145=16*8+17
и т.д
ответ : А=16
3 примера во вложений,напишите,я ещё сделаю
⚡