Пошаговое объяснение:
1) Координаты середины отрезка - это среднее арифметическое от координат концов отрезка.
C( (-3+5)/2 ; (-4-2)/2 ) = (2/2; -6/2) = (1; -3)
2) Радиус окружности - это расстояние между ее центром и точкой B.
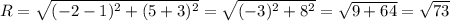
Уравнение окружности
(x-x0)^2 + (y-y0)^2 = R^2, где (x0; y0) - координаты точки О.
(x-1)^2 + (y+3)^2 = 73
3) Точка М сдвинута от точки N на такое же расстояние и в том же направлении, как точка F от точки К.
F(K-2; K-1) = (8-2; -1-1) = (6; -2)
M(N-2; N-1) = (5-2; 5-1) = (3; 4)
ответ: M(3; 4)
4) Уравнение прямой по двум точкам
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
(x + 3)/(2 + 3) = (y - 15)/(-1 - 15)
(x + 3)/5 = -(y - 15)/16
Это каноническое уравнение.
Можно преобразовать в общий вид ax + by + c = 0
16(x + 3) = -5(y - 15)
16x + 48 = -5y + 75
16x + 5y - 27 = 0
Или в вид с угловым коэффициентом y = kx + b
5y = -16x + 27
y = -16x/5 + 27/5
5) Нужно найти точку на оси ординат, то есть x = 0, которая лежит на одинаковом расстоянии от точек М и N. Это точка А(0; y)
|AM| = |AN|
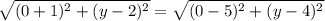
Избавляемся от корней и раскрываем скобки
1 + y^2 - 4y + 4 = 25 + y^2 - 8y + 16
Приводим подобные
8y - 4y = 36
y = 36/4 = 9
ответ: (0; 9)
6) Если прямые параллельны, то коэффициенты при х одинаковы.
Уравнение имеет вид: y = 7x + b
Теперь окружность. Приведем уравнение к обычному виду.
x^2 + y^2 - 10x - 2y + 20 = 0
(x^2 - 10x + 25) - 25 + (y^2 - 2y + 1) - 1 + 20 = 0
(x - 5)^2 + (y - 1)^2 = 6
Центр этой окружности O(5; 1)
Уравнение прямой (x - 5)/1 = (y - 1)/7
7(x - 5) = y - 1
y = 7x - 35 + 1
ответ: y = 7x - 34
ответ:
пошаговое объяснение: отрезки ав и сd пересекаются в точке о , которая является серединой каждого из них.
а) докажите , что треугольник аос=треугольнику bod.
решение: треугольники равны по двум сторонам и углу между ними, так как со=оd, ао=во (дано) и
что и требовалось доказать.
б) найдите угол оас ,если угол оdb =20 градусов, угол аос =115 градусов.
решение: в равных треугольниках против равных сторон лежат равные углы. значит
ответ:
№3) в равнобедренном треугольнике с периметром 64 см одна из сторон рана 16 см. найдите длину боковой стороны треугольника.
решение:
две оставшиеся стороны в сумме равны 64-16=48см. предположим, что это боковые (равные) стороны. тогда боковая сторона равна 24см. если же боковая сторона равна 16см, то основание равно 64-2*16=32см. такой треугольник по теореме о неравенстве треугольников (большая сторона треугольника меньше суммы двух других его сторон) не существует (так как 16+16=32).
ответ: боковая сторона равна 24см.
№1) в треугольнике авс высота вd делит угол в на два угла,причем угол авd=40 градусов, угол свd=10 градусов.
а) докажите ,что треугольник авс - равнобедренный,и укажите его основание.
решение: в прямоугольном (bd-высота) треугольнике dbc
б) высоты данного треугольника пересекаются в точке о.найдите угол вос.
решение: треугольник авс равнобедренный. проведем высоту ае на его основание. треугольник вос также равнобедренный, так как любая точка на высоте ае равноудалена от точек в и с. следовательно
ответ:
№2. отрезки ав и сd пересекаются в точке о,которая является серединой каждого их них.
а)докажите равенство треугольников асв и вdа.
решение: четырехугольник асвd - параллелограмм по признаку: "если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм". следовательно, треугольники асв и вdа равны по трем сторонам, так как в параллелограмме противоположные стороны равны, а сторона ав у них общая. что и требовалось.
б) найдите угол асв,если угол свd=68 градусов.
в параллелограмме углы, прилежащие к одной стороне, в сумме равны 180°. значит
ответ:
№3. две стороны треугольника равны 0,9 см и 4,9 см.найдите длину третьей стороны,если она выражается целым числом сантиметров.
по теореме о неравенстве треугольника, треугольник существует, если сумма двух его сторон больше третьей стороны. 0,9+4,9=5,8. значит третья сторона, удовлетворяющая условию, что ее длина выражается целым числом сантиметров, равна 5см.
ответ: 5см.