√26sin(α+π/2), если ctgα=-5 , 0°<α<180°. Не могу понять как выбрать знак при косинусе ведь он лежит между 180 и 0
Пошаговое объяснение:
{ctgα=-5 ( котангенс отрицателен во 2и 4 четвертях)
{ 0°<α<180° ( это 1 и 2 четверти)
Из этих двух условий следует , что α∈ II четверти. Во 2 четверти cosα<0.
√26sin(α+π/2)= √26cosα
Т.к 1+ctg²α=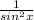
, то 1+(-5)²=
, sin²α=1/26.
По основному тригонометрическому тождеству
sin²α+cos²α=1
1/26+cos²α=1
cos²α=1-1/26
cos²α=25/26
cosα= -√(25/26) , cosα= -5/√26.
√26sin(α+π/2)= √26cosα= √26*(-5/√26)= -5
Объем призмы ищется по такой формуле:
V = Sосн * h, где Sосн — площадь основания призмы, h — ее высота.
Так как все ребра призмы равны, то h = 6 см и в ее основании лежит равносторонний треугольник. Площадь равностороннего треугольника можно найти по следующей формуле:
S = a²√3 / 4, где a — сторона треугольника.
Воспользуемся ей и найдем площадь основания призмы, зная, что a = 6 см:
Sосн = 6²√3 / 4 = 9√3 см².
Теперь можно найти объем призмы:
V = 9√3 * 6 = 54√3 ≈ 93,5 см³.
ответ: объем прямой треугольной призмы равен примерно 93,5 см³.
Пошаговое объяснение: