Математика: решить эту дробь 5х-7 4х-3 = х-3 х

решить эту дробь
5х-7 4х-3
=
х-3 х

👇

Увидеть ответ

Ответ:

pershikovanata

18.11.2020

Пошаговое объяснение:

5x - 7 = 4x - 3

5x - 4x = - 3 + 7

x = 4

x - 3 = x

x - x = 3

0 = 3

4,4(4 оценок)

Открыть все ответы

Ответ:

ПростоПапаЮра

18.11.2020

Креще́ние — первое и важнейшее христианское таинство. Признаётся всеми христианскимиконфессиями, хотя и не в одинаковом смысле.

Через крещение человек становится членом Церкви. Только после крещения человек получает возможность участвовать во всех остальных церковных таинствах, и прежде всего, в евхаристии. Таинство крещения состоит либо в погружении (однократном или троекратном — в зависимости от конфессии) человека в воду, либо в обливании принимающего крещение человека, с произношением священником установленных молитв.
Молитва — обращение верующего к Богу, богам, другим сверхъестественным существам, а также канонизированный текст этого обращения.

4,7(22 оценок)

Ответ:

elinashovhalova

18.11.2020

при a ∈ (3 - √10 ; 3 + √10)

Пошаговое объяснение:

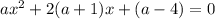
ax^2+2(a+1)x+(a-4)=0

Перед нами квадратное уравнение. Попробуем рассчитать его дискриминант:

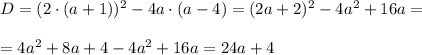
$D=(2\cdot(a+1))^2-4a\cdot(a-4)=(2a+2)^2-4a^2+16a=\\\\=4a^2+8a+4-4a^2+16a=24a+4$

Квадратное уравнение имеет два корня лишь в том случае, когда значение дискриминанта больше нуля. Следовательно:

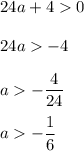
$24a+40\\\\24a-4\\\\a-\dfrac{4}{24}\\\\a-\dfrac{1}{6}$

В таком случае уравнение имеет два корня. Они будут следующие:

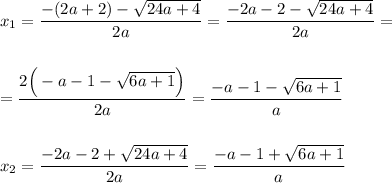
$x_1=\dfrac{-(2a+2)-\sqrt{24a+4}}{2a}=\dfrac{-2a-2-\sqrt{24a+4}}{2a}=\\\\\\=\dfrac{2\Big(-a-1-\sqrt{6a+1}\Big)}{2a}=\dfrac{-a-1-\sqrt{6a+1}}{a}\\\\\\x_2=\dfrac{-2a-2+\sqrt{24a+4}}{2a}=\dfrac{-a-1+\sqrt{6a+1}}{a}$

Теперь рассчитаем расстояние между корнями:

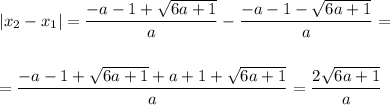
$|x_2-x_1|=\dfrac{-a-1+\sqrt{6a+1}}{a}-\dfrac{-a-1-\sqrt{6a+1}}{a}=\\\\\\=\dfrac{-a-1+\sqrt{6a+1}+a+1+\sqrt{6a+1}}{a}=\dfrac{2\sqrt{6a+1}}{a}$

Нам нужно, чтобы расстояние между корнями было больше 2, следовательно:

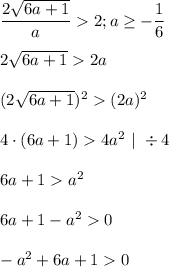
$\dfrac{2\sqrt{6a+1}}{a}2; a\geq -\dfrac{1}{6}\\\\2\sqrt{6a+1}2a\\\\(2\sqrt{6a+1})^2(2a)^2\\\\4\cdot(6a+1)4a^2\ |\ \div4\\\\6a+1a^2\\\\6a+1-a^20\\\\-a^2+6a+10$

Чтобы решить получившееся неравенство, для начала решим соответствующее уравнение:

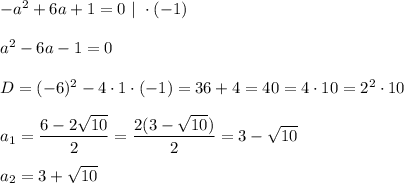
$-a^2+6a+1=0\ |\ \cdot(-1)\\\\a^2-6a-1=0\\\\D=(-6)^2-4\cdot1\cdot(-1)=36+4=40=4\cdot10=2^2\cdot10\\\\a_1=\dfrac{6-2\sqrt{10}}{2}=\dfrac{2(3-\sqrt{10})}{2}=3-\sqrt{10}\\\\a_2=3+\sqrt{10}$