Відповідь:
Искомая комбинация целых последовательных чисел 77, 78 и 79, которые при перемножении дают шестизначный палиндром вида 474474. Сумма этих трех чисел равна 77 + 78 + 79 = 234.
Покрокове пояснення:
Шестизначное число - палиндром, начинающееся на 47 имеет вид: 47ХХ74, где Х любая цифра от 0 до 9.
Примечание: Вычисление корней из чисел я произвожу с точностью до третьего знака после запятой.
Корень квадратный из числа 470074 равен 685,600.
Корень квадратный из числа 479974 равен 692,782.
Значит нам надо умножить два последовательных целых числа, которые находятся рядом с числами из интервала от 685 и до 693, чтобы получить требуемый шестизначный палиндром.
Таких чисел не существуют, перемножение двух соседних чисел не даёт требуемого результата.
Корень кубический из числа 470074 равен 77,754.
Корень кубический из числа 479974 равен 78,296.
Значит нам надо умножить три последовательных целых числа, которые находятся рядом с числом 77 или 78, чтобы получить требуемый шестизначный палиндром.
Такие числа существуют, это 77, 78 и 79.
77 × 78 × 79 = 474474
77 + 78 + 79 = 234
Корень четвертой степени из числа 470074 равен 26,184.
Корень четвертой степени из числа 479974 равен 26,321.
Значит нам надо умножить четыре последовательных целых числа, которые находятся рядом с числом 26, чтобы получить требуемый шестизначный палиндром.
Таких чисел не существуют, перемножение четырех соседних чисел не даёт требуемого результата.
24 × 25 × 26 × 27 = 421200
25 × 26 × 27 × 28 = 491400
Перемножение дает числа далеко отстоящие от числа вида 47ХХ74. Это происходит и при увеличении количества перемножаемых чисел.
Вывод: существует только одна комбинация целых последовательных чисел 77, 78 и 79, которые при перемножении дают шестизначный палиндром вида 47ХХ74. Сумма этих трех чисел равна 77 + 78 + 79 = 234.
Это показательное уравнение вида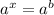 
, где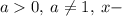 
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения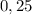 
представить в виде числа со степенью так, чтобы в основании было число 
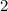. Это явно число 
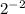(проверка: 
).
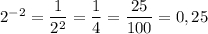Значит теперь, когда наше показательное уравнение имеет вид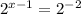 
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение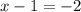 
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 
.
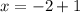Из этого следует, что ответ нашего показательного уравнения равен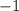 
.
Пошаговое объяснение:
решение на фото