Оценим максимальное значение, которое может принимать элемент множества 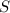 . Предположим, что существуют хотя бы два элемента множества, больших
. Предположим, что существуют хотя бы два элемента множества, больших 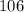 . Пусть это числа
. Пусть это числа 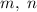 . Положим
. Положим 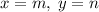 , тогда
, тогда 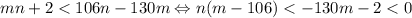 , откуда
, откуда 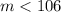 . Противоречие. Значит, существует не более одного числа, большего
. Противоречие. Значит, существует не более одного числа, большего
Теперь становится ясно, как строить множество. Пусть максимальное число равно 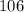 . Тогда следующее по величине число меньше
. Тогда следующее по величине число меньше 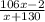 , где
, где  — текущее число (сейчас рассматривается максимальное число; оценка следует из исходного уравнения). То есть второе по величине число не превосходит
— текущее число (сейчас рассматривается максимальное число; оценка следует из исходного уравнения). То есть второе по величине число не превосходит 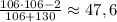 . Берем 47. Далее:
. Берем 47. Далее: 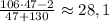 . Берем 28. И так далее. Получим множество
. Берем 28. И так далее. Получим множество 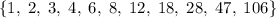 , состоящее из 11 элементов. Это и есть наш ответ.
, состоящее из 11 элементов. Это и есть наш ответ.
Пішохід йшов 2 год зі швидкістю 4,2 км/год і 3 год зі швидкістю 4,7 км/год. З якою сталою швидкістю він мав іти, щоб подолати ту саму відстань за той самий час?
Розв’язання. Знайдемо відстань, що пройшов пішохід: 4,2 ∙ 2 + 4,7 ∙ 3 = 22,5 км. Розділимо це значення на використаний час: 22,5 : 5 = 4,5 км/год. Отже, пішохід мав йти зі сталою швидкістю 4,5 км/год.
Таку швидкість називають середньою швидкістю руху. Цю саму відповідь можна було б одержати, якщо знайти середнє арифметичне швидкостей за кожну годину руху:
(4,2 + 4,2 + 4,7 + 4,7 + 4,7) : 5 = 4,5 км/год.
Отже, щоб знайти середню швидкість руху, треба весь пройдений шлях поділити на весь затрачений час.
Пошаговое объяснение:
............................