Серый Волк и Иван-царевич шли добывать Живую Воду. Иван всё время шёл с постоянной скоростью — 3 км/ч. Волк же сперва шёл рядом, но
в 13.50 убежал вперёд — проверить, нет ли у колодца с Живой Водой какой-либо
опасности. Он увеличил скорость до 5 км/час, добежал до колодца, мгновенно всё
проверил и побежал обратно, встретив Ивана в 14.05. Дальше Иван шёл один. В какое
время был у колодца: а) Серый Волк? б) Иван-царевич?

👇

Увидеть ответ

Открыть все ответы

Ответ:

Fogles12

07.01.2022

1). Первое число.

Вначале сделаем некоторые упрощения (основные свойства корней и степеней, фактически никаких подсчетов):

$\displaystyle 0,6^{\frac{1}{3} } \cdot 1,3 ^{- \frac{2}{5} } = \sqrt[3]{0,6^1} \cdot \frac{1}{1,3 ^ \frac{2}{5} } = \sqrt[3]{0,6} \cdot \frac{1}{ \sqrt[5]{1,3^2} } = \sqrt[3]{0,6} \cdot \sqrt[5]{\frac{1}{{1,3^2} } } =\\\\= \sqrt[15]{0,6^5} \cdot \sqrt[15]{\frac{1^3}{1,3^6 } } = \sqrt[15]{ \frac{0,6^5}{1,3^6} }$

А теперь можно либо посчитать, что находится под корнем, либо избежать муторных вычислений и сразу сказать, что числитель меньше знаменателя, и дробь меньше единицы. Значит, и корень из такой дроби тоже меньше единицы.

Итог: число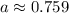 $a \approx 0.759$ не подходит.

2). Второе число.

Расписываю менее подробно:

$\displaystyle 0,7^{- \frac{2}{3} } \cdot 0,3^{- \frac{1}{5} } = \sqrt[3]{\frac{1}{0,7^2} } \cdot \sqrt[5]{\frac{1}{0,3^1} } = \sqrt[15]{\frac{1}{0,7^{10}} } \cdot \sqrt[15]{\frac{1}{0,3^3} } = \sqrt[15]{ \frac{1}{0,7^{10} \cdot 0,3^3} }$

Очевидно, что знаменатель в подкоренном выражении меньше единицы, поэтому само подкоренное выражение больше единицы. И корень больше единицы.

Итог: число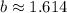 $b \approx 1.614$ подходит.

3). Третье число.

И, наконец, последнее число:

$\displaystyle 1,8^{\frac{1}{3} } \cdot 0,3^{-\frac{2}{5} } = \sqrt[3]{1,8} \cdot \sqrt[5]{\frac{1}{0,3^2} } = \sqrt[15]{1,8^5} \cdot \sqrt[15]{\frac{1}{0,3^6} } = \sqrt[15]{ \frac {1,8^5}{0,3^6} }$

Здесь, опять, подкоренное выражение больше единицы (по вполне понятным причинам), так что и сам корень будет больше единицы.

Итог: число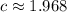 $c \approx 1.968$ подходит.

ответ: b и c.

4,5(29 оценок)

Ответ:

VladiusFirst

07.01.2022

Слово «длиНа» пишется с одной «н».

ПЕРВАЯ ЗАДАЧА
1) 18 - 6 = 12 см - ширина исходного прямоугольника.
2) 18•12 = 216 кв.см площадь исходного прямоугольника.
3) Примем за 1 часть площадь меньшего прямоугольника, образовавшегося при разделении исходного прямоугольника на две неравные части.
Тогда
5•1 = 5 частей соответствуют площади большего треугольника, образовавшегося при разделении исходного прямоугольника на две неравные части.
5 + 1 = 6 частей соответствуют площади исходного прямоугольника.
4) 216 : 6 = 36 кв, см - площадь одной части и соответственно меньшего прямоугольника, а также площадь квадрата равного по площади меньшему прямоугольника
5) √36 = 6 см сторона квадрата, равного по площади меньшему прямоугольнику.
6) 4•6 = 24 см периметр квадрата, равного по площади меньшему прямоугольнику.
ответ: 24 см.

ВТОРАЯ ЗАДАЧА
1) 12 + 15 = 27 см - длина исходного прямоугольника.
2) 27•12 = 324 кв.см площадь исходного прямоугольника.
3) Примем за 1 часть площадь меньшего прямоугольника, образовавшегося при разделении исходного прямоугольника на две неравные части.
Тогда
3•1 = 3 части соответствуют площади большего треугольника, образовавшегося при разделении исходного прямоугольника на две неравные части.
3 + 1 = 4 частей соответствуют площади исходного прямоугольника.
4) 324 : 4 = 81 кв, см - площадь одной части и соответственно меньшего прямоугольника, а также площадь квадрата равного по площади меньшему прямоугольника
5) √81 = 9 см сторона квадрата, равного по площади меньшему прямоугольнику.
6) 4•9 = 36 см периметр квадрата, равного по площади меньшему прямоугольнику.
ответ: 36 см.

4,7(72 оценок)

Это интересно:

Кулинария-и-гостеприимство

08.08.2020

Как варить рыбу: секреты приготовления вкусной и полезной блюда...

Кулинария-и-гостеприимство

18.10.2020

Как сделать пробку, проткнуть или разрезать корку арбуза...

Компьютеры-и-электроника

22.06.2021

Как легко управлять своими фотографиями с помощью программы Picasa...

Питомцы-и-животные