Пошаговое объяснение:
приведем квадратичную форму
B = x² + 9y²
к главным осям, то есть к каноническому виду
матрица этой квадратичной формы
1 0
0 9
собственные числа и собственные векторы этой матрицы
(1 - λ)x + 0y = 0
0x + (9 - λ)y = 0
характеристическое уравнение
λ² - 10λ + 9 = 0
D=(-10)² - 4*1*9=64
λ₁ = 9; λ₂ = 1
поскольку λ₁ > 0; λ₂ > 0, это эллипс
квадратичная форма
х² +9у²
выделим полные квадраты
для х
(x²-2*20x + 20²) -1*20² = (x-20)²-400
для y
9(y²+2*2y + 2²) -9*22 = 9(y+2)²-36
и получим
(x-20)²+9(y+2)² = 336
делим все на 336
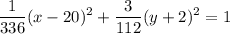
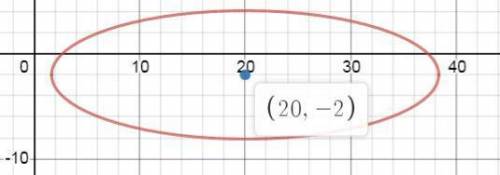
эллипс с центром в точке С(20; -2)
полуоси

фокусы
координаты фокусов F₁(-c;0) и F₂(c;0), где c - половина расстояния между фокусами
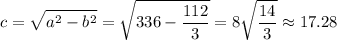
и тогда фокусы
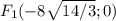
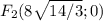
с учетом центра фокусы будут
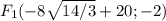
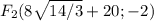
РЕШЕНИЕ
ДАНО
Всего = 25
Зеленых = 5
Красных = 20
РЕШЕНИЕ
а) Номер 4 = 1 из 25 = 1/25 = 0,25 = 4% - ОТВЕТ
b) Два события = И "№ 4" И "зеленый" - произведение вероятностей
Р(b) = 1/25 * 5/25 = 5/125 = 1/25 = 0,04 = 4% - ОТВЕТ
c) Три события = И "№4" И "зеленый" и "ЧЕТНЫЙ"
Вероятность четного = 0,5
P(c) = 1/25 * 5/25 * 0,5 = 1/ 250 =0,004 = 0,4% - ОТВЕТ
ЗАДАЧА 2 - рыба
Три наживки, но события НЕ зависимые - ИЛИ
Вероятности суммируются
Р(2) = 1/3* 0,5 + 1/3 *0,6 +1/3 *0,7= 1/6+1/5+7/30 = 3/5 = 0,6 = 60%