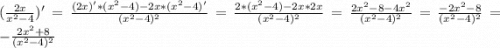Доказательство делимости на 2 - если запись целого числа оканчивается одной из цифр 0, 2, 4, 6, 8, то это число делится на 2 нацело. доказательство делимости на 5 - если в записи целого числа справа находится цифра 0 или 5, то такое число делится на 5. доказательство делимости на 4 - чтобы проверить, делится ли на 4 данное однозначное натуральное число, проще всего выполнить деление непосредственно, из однозначных чисел на 4 делятся только 4 и 8. разделить двузначное натуральное число на 4 также не составит труда (даже при устном делении). например, 24 делится на 4 без остатка, так как 24: 4=6, а 83 не делится нацело на 4, так как 83: 4=20 (ост. 3) (при необходимости смотрите статьи правила и примеры деления натуральных чисел и правила и примеры деления натуральных чисел с остатком). но чем больше цифр содержится в записи числа, тем «неприятнее» проводить деление. доказательство делимости на 25 - если число заканчивается на 00, 25, 50 или 75, то оно делится на 25 нацело. доказательство делимости на 3 - целое число делится на 3, если сумма его цифр делится на 3, если же сумма цифр данного числа не делится на 3, то и само число не делится на 3. на 3 делятся числа 3, 6 и 9. доказательство делимости на 9 - если сумма цифр целого числа делится на 9, то и само число делится на 9; если же сумма цифр числа не делится на 9, то это число не делится на 9.
Решение Действительное число называется действительной частью комплексного числа z = a + bi . Действительное число называется мнимой частью числа z = a + bi . найти мнимую и действительную части комплексного числа (2+7i) (l-i) = 2 - 2i + 7 - 7i² = 9 - 2i + 7 = 16 - 2i [i² = - 1] 16 - действительное число; - 2 - мнимая часть i(5+2i) = 5i + 2i² = - 2 + 5i - 2 - действительное число; 5 - мнимая часть (1+4i) (2-8i) = 2 - 8i + 8i - 32i² = 2 + 32 = 34 34 - натуральное число и у него нет мнимой и действительной частей комплексного числа (5+2i)² = 25 + 20i + 4i² = 25 + 20i - 4 = 21 + 20i 21 - действительное число; 20 - мнимая часть
Відповідь:
Покрокове пояснення:
3.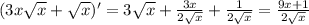
4.