Например у нас есть действие 34*2 =
Потом давай по сложнее.
46*73=
Ты построил(а) столбик. Теперь умножаем. 46 нужно умножить на 3, и всегда умножение в столбик, сначала выполняем с самой правой цифрой. И так. 6 умножаем на 3 ровно 18. Пишем 8. А цифру 1 ставим над цифрой 4. Теперь 4 умножаем на 3 ровно 12, и мы ставили 1 над 4 значит 1 прибавляем к 12, получается 13. 13 пишем полностью. У нас получилось число 138. Но это ещё не всё. Теперь нужно ещё раз умножить, но сейчас уже на другое число. Умножаем 46 на 7. Так же по одной цифре. 6 умножить на 7 будет 42. Пишем 2, и 4 над четвёркой. Теперь, 4 умножаем на 7. Будет 28, но мы подписывали 4 под четвёркой. Значит к 28-ми прибавляем 4. Получается 32. Пишем 32. Получается число 322. А теперь прибавляем. 138 + 322 = 3358.
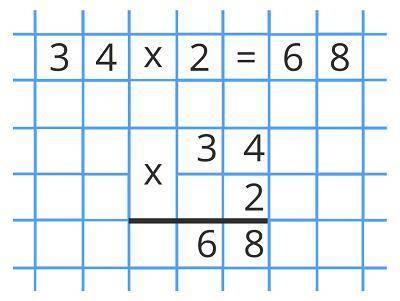
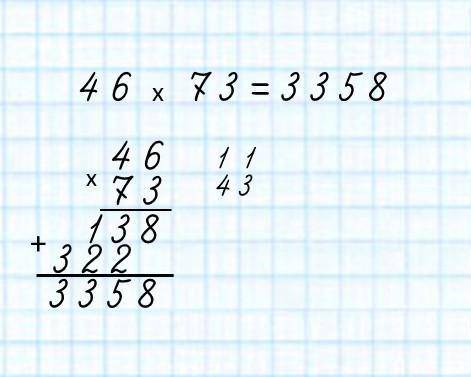
1) 2^8+4^5-8^2=2^8+(2^2)^5-(2^3)^2=2^8+2^10-2^6=2^6*(2^2+2^4-1)=2^6*(4+16-1)=2^6*19=2^5*(2*19)=2^5*38 это выражение делится на 38
(2^5*38)/38=2^5=32 что требовалось доказать
2) 3^11+9^6+27^3=3^11+(3^2)^6+(3^3)^3=3^11+3^12+3^9=3^9*(3^2+3^3+1)=3^9*(9+27+1)=3^9*37=3^8*(3*37)=3^8*111 это выражение делится на 111
(3^8*111)/111=3^8 что требовалось доказать
3) a=9^7+9^6+9^5=(3^2)^7+(3^2)^6+(3^2)^5=3^14+3^12+3^10=3^10*(3^4+3^2+1)=3^10*(81+9+1)=3^10*91.
b=3^10-3^9+3^8=3^8*(3^2-3+1)=3^8*(9-3+1)=3^8*7
(3^10*91)/(3^8*7)=3^2*91/7=9*13=117 что и требовалось доказать а делится на b