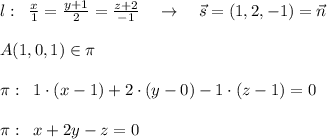
, лежит на перпендикуляре, проведённым из точки А к этой прямой. можно провести в плоскости, перпендикулярной прямой . будет нормальным вектором плоскости и точка А лежит в этой плоскости.
и плоскости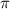 
. 
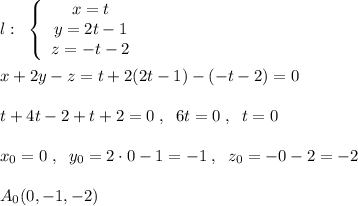
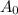является серединой отрезка 
.
.
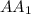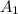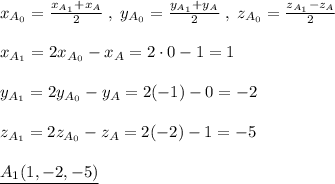
Пошаговое объяснение:
(c+4 8/21)-7 13/21=2 12/21
С=2 12/21+7 13/21-4 8/21
С=5 17/21