Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
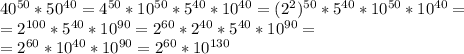
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
2.15 монет снова делим на три части. находим в которых их 5 монет тяжелее.
3. их пяти монет сравниваем 2 и 2. если одинаковые- пятая монета тяжелее, если разный вес - 4 взвешивание
4. сравниваем две монеты - тяжелая найдена.
2)если модуль равен нулю, выражение равно только 0, модуль можно отбрасывать
2x-1=0
х=1/2
х=0,5
8+5х=0
5х=-8
х=-8/5=1 3/5=1,6
7-2х=0
2х=7
х=7/2
х=3,5
9х-4=0
9х=4
х=4/9