1. Имеется три партии ламп по 100, 200 и 300 штук. В первой партии 80% ламп с
продолжительностью работы более 1 000 часов, во второй - 75%, в третьей – 60%.
Какова вероятность, что случайно выбранная лампа, проработавшая более 1000 часов, была взята из второй партии?
2. Получить ряд распределения для случайной величины – числа попаданий в цель при двух выстрелах, если вероятность попадания в цель равна 0.8 при одном выстреле. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины. Построить график функции распределения и показать на нем математическое ожидание и среднее квадратическое отклонение.
Пошаговое объяснение:
1. Имеется три партии ламп по 100, 200 и 300 штук. В первой партии 80% ламп с
продолжительностью работы более 1 000 часов, во второй - 75%, в третьей – 60%.
Какова вероятность, что случайно выбранная лампа, проработавшая более 1000 часов, была взята из второй партии?
2. Получить ряд распределения для случайной величины – числа попаданий в цель при двух выстрелах, если вероятность попадания в цель равна 0.8 при одном выстреле. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины. Построить график функции распределения и показать на нем математическое ожидание и среднее квадратическое отклонение.
0,33
Пошаговое объяснение:
4/52 = 1/13 - вероятность выбрать взять карту «короля»
теперь надо расписать все возможные варианты для 5 карт
К - король; Х - не король:
вообще в данном случае много вариантов, поэтому я напишу только один вариант, который не подходит, ведь только при одном варианте королей вообще не будет: Х Х Х Х Х
вероятность этого события надо вычислить и вычесть и 1 (100%)
вероятность достать карту не с королем = 1 - 1/13 = 12/13
так как мы достаем 5 карт, то вероятность (Х Х Х Х Х) =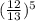
что примерно равняется 0,67
теперь из 100% вычитаем полученные 67%
1 - 0,67 = 0,33