В треугольнике АВС ВД биссектриса и ВД = 12, АВ = 14 , ВС = 35.
1.Проведем через точку Д прямую параллельную АВ и точка Р ВС. Получаем, что треугольник ВРД равнобедренный ( ВДР = ) и ВР = ДР.
2. АВС подобен ДРС ( по двум углам) АВ / РД = 7/5 14/РД = 7/ 5 и РД=10 и
ВР = 10.
3. В ВДР найдем cos BDP по теореме косинусов, cos BDP = 0,6 ,
значит sin BDP = sin ABD = 0, 8.
4. Т. К. ВД биссектриса ,то по свойству биссектрисы: АД / ДС = 14/ 35 = 2/5 и SABD / SBDC =2/5 SABD = 2/7 SABC .
SABD = ½ AB BD sin ABD = 67,5, значит SABC = 7/2 SABD = =235.2. ответ : 235,2.
Формула Эйлера для многогранников.
Пусть В — число вершин выпуклого многогранника, Р — число его ребер и Г — число граней. Тогда верно равенство В+Г=Р+2.
Октаэдр - многогранник с 8 гранями. (Грани- треугольники)У него 6 вершин и 12 ребер.
8+6=12+2. Формула Эйлера верна.
Додекаэдр - многогранник, состоящий из граней- пятиугольников.Этих граней 12.У него 30 ребер и 20 вершин.
20+12=30+2 Формула Эйлера верна.
Икосаэдр - многогранник, состоящий из 20 граней-треугольников.
У него также, как и у додекадра,
30 ребер и 20 вершин.
20+12=30+2 Формула Эйлера верна.
Пошаговое объяснение:
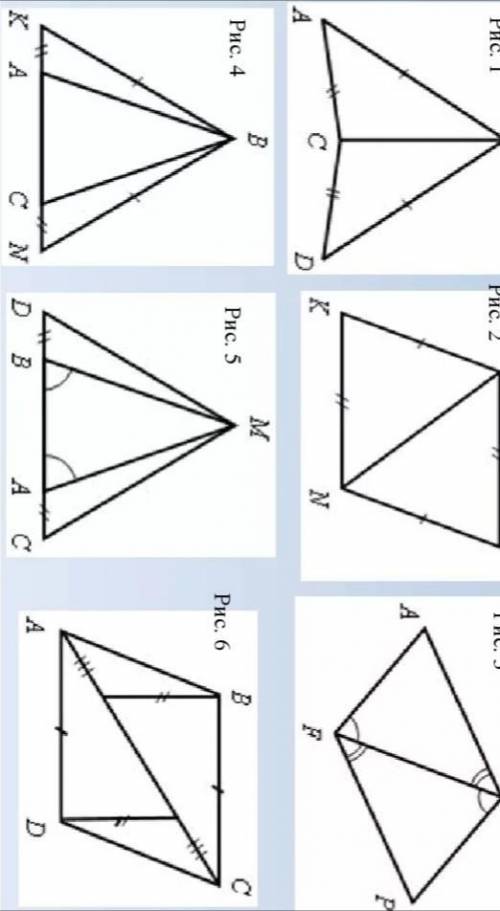
1. ΔBAD=ΔDCB - прямоугольные (по условию), равны по катету AB=CD и гипотенузе BD - общая сторона.
2. ΔКТМ=ΔКТN - прямоугольные (по условию), равны по двум катетам MT=TN (по условию), KT - общий катет.
3. ΔPKS=ΔRKS - прямоугольные, так как ∠PKS=∠RKS (по условию) - смежные, значит ∠PKS=∠RKS=90°. Треугольники равны по общему катету KS и острому углу ∠KPS=∠KRS (по условию).
4. ΔERF=ΔESF - прямоугольные (по условию), равны по общей гипотенузе EF и острому углу ∠REF=∠SEF (по условию).
5. ΔSPM=ΔTKM - прямоугольные (по условию), равны по катету SP=KT (по условию) и гипотенузе SM=TM (по условию).
ΔRPM=ΔRKM - прямоугольные, равны по катету РМ=КМ (из равенства ΔSPM=ΔTKM) и общей гипотенузе RM.