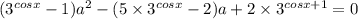
8/Задание № 5:
Пловец по течению быстрой реки проплыл 180 м. Когда же он поплыл против течения, то за такое же время его снесло течением на 60 м ниже по течению. Во сколько раз скорость течения реки больше скорости пловца?
РЕШЕНИЕ: Пусть скорость пловца х, а скорость течения у.
В первый раз за время t он проплыл расстояние 180=(y+x)t.
Во второй раз за такое же время t его снесло на расстояние 60=(y-x)t.
Выражаем t в обоих случаях: 180/(y+x)=60/(y-x)
3/(y+x)=1/(y-x)
3(у-x)=(у+x)
3y-3x=x+y
2y=4x
y=2x
Скорость течения реки больше скорости пловца в 2 раза.
ОТВЕТ: в 2 раза
8/Задание № 5:
Пловец по течению быстрой реки проплыл 180 м. Когда же он поплыл против течения, то за такое же время его снесло течением на 60 м ниже по течению. Во сколько раз скорость течения реки больше скорости пловца?
РЕШЕНИЕ: Пусть скорость пловца х, а скорость течения у.
В первый раз за время t он проплыл расстояние 180=(y+x)t.
Во второй раз за такое же время t его снесло на расстояние 60=(y-x)t.
Выражаем t в обоих случаях: 180/(y+x)=60/(y-x)
3/(y+x)=1/(y-x)
3(у-x)=(у+x)
3y-3x=x+y
2y=4x
y=2x
Скорость течения реки больше скорости пловца в 2 раза.
ОТВЕТ: в 2 раза
Відповідь:
Покрокове пояснення:
Пусть у=3^sinx
Тогда уравнение имеет вид
(у-1)а^2-(5у-2)а+2×3×у=0
Раскроем скобки и сгруппируем
уа^2-а^2-5уа+2а+6у=0
у(а^2-5а+6)-а(а-2)=0
корни а^2-5а+6=0 есть 2 и 3
у(а-2)(а-3)-а(а-2)=0
(а-2)(у(а-3)-а)=0
а=2 или уа-3у-а=0 → а=3у/(у-1)
а=2 или а= 3^(sin x +1)/(3^sin x-1) & x≠pi×n