Чтобы запечь одну утку требуется 2 часа
1/2 это половина утки
значит
2÷2=1
ответ: нужно 1 час чтобы запеч
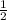
утку
1) x x A B
= = + ;
x²-5x+6 (x-2)(x-3) x-2 x-3
При х=2: А=2/(-1)=-2. При х=3: В=3/1=3.
х dx dx dx
∫ = -2 ∫ + 3 ∫ = -2ln|x-2| +3ln|x-3| +C
x²-5x+6 x-2 x-3
2) z=cos(xy)
z¹(по х) = -sin(xy) *y= -y*sin(xy)
z¹(по у)= -sin(xy) *x= -x*sin(xy)
3) z=√(xy) y
z¹(по х)= 1/ (2√(xy) ) *y=
2√(xy)
х
z¹(по у)=
сорь если не так знение плохое
ответ:Воспользуемся формулой Лапласа
вероятность, что событие наступит k раз при n испытаниях
P(k) = 1/корень (npq) * ф [ (k-np)/корень (npq) ], где
p - вероятность события, q = 1-p, ф - функция Гаусса
ф (x) = 1/корень (2pi) * e^(-x^2 / 2)
n = 1600, k = 1200, p = 0.8, q = 0.2
np = 1280, корень (npq) = 16
x = (k-np)/корень (npq) = -80 / 16 = -5
ф = 1/корень (2pi) * e^(-x^2 / 2) = 0.3989 * e^(-12.5) = 0,3989*3,731*10^(-6) = 1.488*10^(-6)
P(1200) = 1/16 * 1.488*10^(-6) = 0.93*10^(-7)
вероятность ничтожно мала - меньше одной десятимиллионной
Пошаговое объяснение:Воспользуемся формулой Лапласа
вероятность, что событие наступит k раз при n испытаниях
P(k) = 1/корень (npq) * ф [ (k-np)/корень (npq) ], где
p - вероятность события, q = 1-p, ф - функция Гаусса
ф (x) = 1/корень (2pi) * e^(-x^2 / 2)
n = 1600, k = 1200, p = 0.8, q = 0.2
np = 1280, корень (npq) = 16
x = (k-np)/корень (npq) = -80 / 16 = -5
ф = 1/корень (2pi) * e^(-x^2 / 2) = 0.3989 * e^(-12.5) = 0,3989*3,731*10^(-6) = 1.488*10^(-6)
P(1200) = 1/16 * 1.488*10^(-6) = 0.93*10^(-7)
вероятность ничтожно мала - меньше одной десятимиллионной