Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Для точек М и А - это длина стороны АМ треугольника АСМ.
СМ - перпендикулярен плоскости АВСD, значит перпендикулярен любой прямой, проходящей через его основание С.⇒
∆ АСМ- прямоугольный.
АМ=√(CM²+AC²)
В данной трапеции АВ =24 (- меньшая боковая сторона),
CD=25.
ВD - биссектриса прямого угла.
∠АВD=45°, следовательно, ∠АDB =45°, ∆ АВD- равнобедренный и AD=AB=24
Опустим из С перпендикуляр СН на АD.
Отношение сторон ∆ СНD – из Пифагоровых троек, НD=7( проверьте).
Тогда ВС=24-7=17.
По т.Пифагора АС²=24²+17²=865
АМ=√(735+865)=√1600=40 (ед. длины)
Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Для точек М и А - это длина стороны АМ треугольника АСМ.
СМ - перпендикулярен плоскости АВСD, значит перпендикулярен любой прямой, проходящей через его основание С.⇒
∆ АСМ- прямоугольный.
АМ=√(CM²+AC²)
В данной трапеции АВ =24 (- меньшая боковая сторона),
CD=25.
ВD - биссектриса прямого угла.
∠АВD=45°, следовательно, ∠АDB =45°, ∆ АВD- равнобедренный и AD=AB=24
Опустим из С перпендикуляр СН на АD.
Отношение сторон ∆ СНD – из Пифагоровых троек, НD=7( проверьте).
Тогда ВС=24-7=17.
По т.Пифагора АС²=24²+17²=865
АМ=√(735+865)=√1600=40 (ед. длины)
Подробнее - на -
a принадлежит второй четверти, в которой косинус отрицателен,
тогда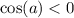
но т.к.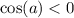 , то
, то
итак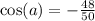
теперь найдем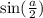 и
и 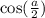 .
.
а это значит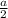 принадлежит первой четверти в которой и синус и косинус положительны, поэтому
принадлежит первой четверти в которой и синус и косинус положительны, поэтому