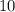 а два черных шара -
а два черных шара - 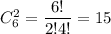 По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)
По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)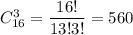
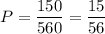
 И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно
И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно 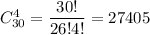

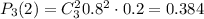
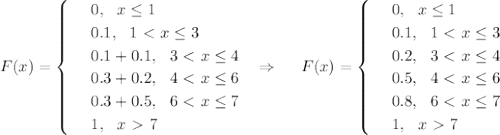
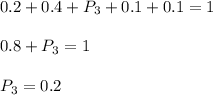


 а два черных шара -
а два черных шара - 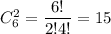 По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)
По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)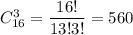
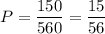
 И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно
И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно 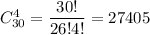

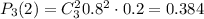



Вася и Петя учатся в школе в одном классе. Недавно Петя поведал Васе о хитром возведения в квадрат натуральных чисел, оканчивающихся на цифру 5. Теперь Вася может с легкостью возводить в квадрат двузначные (и даже некоторые трехзначные) числа, оканчивающиеся на заключается в следующем: для возведения в квадрат числа, оканчивающегося на 5 достаточно умножить число, полученное из исходного вычеркиванием последней пятерки на следующее по порядку число, затем остается лишь приписать «25» к получившемуся результату справа. Например, для того, чтобы возвести число 125 в квадрат достаточно 12 умножить на 13 и приписать 25, т.е. приписывая к числу 12*13=156 число 25, получаем результат 15625, т.е. 1252=15625. Напишите программу, возводящую число, оканчивающееся на 5, в квадрат для того, чтобы Вася смог проверить свои навыки.