\lim_{n \to \infty} \frac{x^2-4x-5}{x^2-2x-3}= [\frac{\infty}{\infty}]=\lim_{n \to \infty} \frac{ \frac{x^2}{x^2}- \frac{4x}{x^2}- \frac{5}{x^2}}{ \frac{x^2}{x^2}- \frac{2x}{x^2}- \frac{3}{x^2}}= \lim_{n \to \infty} \frac{1- \frac{4}{x}- \frac{5}{x^2}}{1- \frac{2}{x}- \frac{3}{x^2}}= \lim_{n \to \infty} \frac{1-0-0}{1-0-0}=1
Второй вариант решения:
\lim_{n \to \infty} \frac{x^2-4x-5}{x^2-2x-3}= [\frac{\infty}{\infty}]= \lim_{n \to \infty} \frac{x^2-4x}{x^2-2x}= \lim_{n \to \infty} \frac{x(x-4)}{x(x-2)} = \lim_{n \to \infty} \frac{x-4}{x-2}= \lim_{n \to \infty} \frac{x}{x}=1
Третий вариант решения:
\lim_{n \to \infty} \frac{x^2-4x-5}{x^2-2x-3}=[\frac{\infty}{\infty}]= \lim_{n \to \infty} \frac{(x^2-4x-5)'}{(x^2-2x-3)'}= \lim_{n \to \infty} \frac{(2x-4)'}{(2x-2)'}= \frac{2}{2}=1
195/506
Пошаговое объяснение:
Занумеруем места в группе.
Всего есть 25 * 24 * 23 * 22 * 21 вариантов групп: на место с номером 1 есть 25 претендентов, на второе может попасть любой из 24 оставшихся и так далее.
Посчитаем, сколько групп на первых трёх местах имеют мальчиков, а на остальных – девочек (обозначу такую группу МММДД). На первое место можно взять любого из 15 мальчиков, на второе – любого из 14, на третье – из 13, на четвёртое есть 10 вариантов, на пятое – 9. Итого 15 * 14 * 13 * 10 * 9 вариантов.
Очевидно, каждый тип группы, удовлетворяющей условию (например, МДМДМ) можно набрать из 15 * 14 * 13 * 10 * 9 вариантов. Всего поставить две Д в строку из пяти букв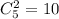 
, так что общее число вариантов групп, в которых 3 мальчика и 2 девочки, равно 10 * 15 * 14 * 13 * 10 * 9
Вероятность есть отношение количества подходящих вариантов к общему числу вариантов:
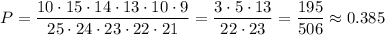
Яблок - 19 кг
Груш - 17 кг
Пакеты - ?
ответ: понадобилось 9 пакетов
Пошаговое объяснение:
(19 + 17) : 4 = 9 (пакетов) - понадобилось
ответ: понадобилось 9 пакетов