N: 25; 2; 9.
Z: -13; -79; -914; -1.
Q: 0.25; 2.9; -4.2;
Пошаговое объяснение:
N - множество натуральных чисел. Числа, возникающие естественным образом при счёте (например, 1, 2, 3, 4, 5, 6, 7, 8, 9…)
Z -- Це́лые чи́сла. Расширение множества натуральных чисел, получаемое добавлением к нему нуля и отрицательных чисел(.... -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5 .....)
Q -- Множество «Q» включает в себя множество целых чисел «Z» и натуральных чисел «N». Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Иными словами любое
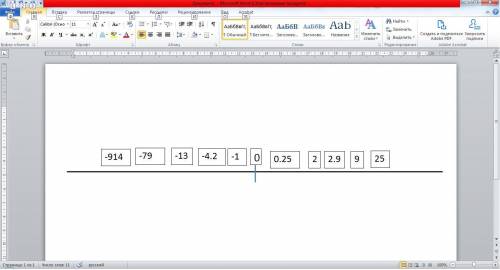
P.S. На графике схематичное изображение чисел
P.S.2 Постарайся писать с пробелами между элементами перечисления
Рассуждения в разделе "Пошаговое объяснение".
Пошаговое объяснение:Признаки делимости числа на 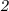 :
:
Число делится на  , если его конечная цифра чётная.
, если его конечная цифра чётная.
Пример: 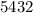 делится на
делится на  , ибо его конечная цифра чётная.
, ибо его конечная цифра чётная.
Признаки делимости числа на 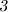 :
:
Число делится на  , если сумма его цифр делится на
, если сумма его цифр делится на  .
.
Пример: 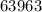 делится на
делится на  , ибо сумма его цифр делится на
, ибо сумма его цифр делится на  .
.
Признаки делимости числа на 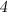 :
:
Число делится на  , если его
, если его  последние цифры нули или образуют число, делящиеся на
последние цифры нули или образуют число, делящиеся на  .
.
Пример: 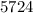 делится на
делится на  , ибо
, ибо  последние цифры (последняя цифра, если число однозначное) образуют число
последние цифры (последняя цифра, если число однозначное) образуют число 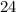 , делящиеся на
, делящиеся на  .
.
Признаки делимости числа на 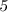 :
:
Число делится на  , если его конечная цифра
, если его конечная цифра 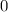 или
или  .
.
Пример: 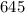 делится на
делится на  , ибо его конечная цифра
, ибо его конечная цифра  .
.
Признаки делимости числа на 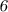 :
:
Число делится на 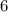 , если конечная цифра чётная и сумма цифр этого числа делится на
, если конечная цифра чётная и сумма цифр этого числа делится на  .
.
Пример: 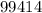 делится на
делится на 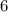 , ибо его конечная цифра
, ибо его конечная цифра  чётная и сумма цифр этого числа делится на
чётная и сумма цифр этого числа делится на  .
.
Признаки делимости числа на 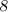 :
:
Число делится на 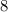 , если
, если  его последние цифры образуют число, делящиеся на
его последние цифры образуют число, делящиеся на 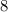 .
.
Пример: 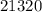 делится на
делится на 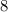 , ибо
, ибо  его последние цифры образуют число
его последние цифры образуют число 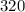 , делящиеся на
, делящиеся на 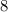 .
.
Признаки делимости числа на 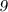 :
:
Число делится на 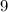 , если сумма его цифр делится на
, если сумма его цифр делится на 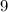 .
.
Пример: 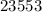 делится на
делится на 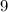 , ибо сумма его цифр делится на
, ибо сумма его цифр делится на 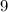 .
.
Признаки делимости числа на  :
:
Число делится на 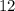 , если оно кратно
, если оно кратно  и
и  .
.
Пример: 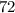 делится на
делится на 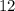 , ибо оно кратно
, ибо оно кратно  и
и  .
.
Признаки делимости числа на 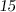 :
:
Число делится на 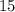 , если его конечная цифра
, если его конечная цифра 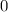 или
или  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
Пример: 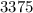 делится на
делится на 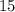 , ибо его конечная цифра
, ибо его конечная цифра  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
------------------------------------------------------------------------------------------------
Какие из чисел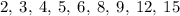 являются делителем
являются делителем 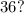
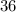 делится на
делится на 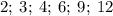 , ибо его конечная цифра чётная, сумма цифр этого числа делится на
, ибо его конечная цифра чётная, сумма цифр этого числа делится на  и
и 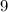 , оно кратно
, оно кратно  и
и  , его
, его  последние цифры образуют число, делящиеся на
последние цифры образуют число, делящиеся на  .
.
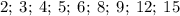 являются кратным
являются кратным 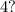
Справедливо неравенство: 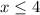 .
.
Числа 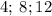 кратны
кратны  , ибо последняя цифра
, ибо последняя цифра 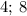 делится/
делится/ последние цифры
последние цифры 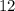 делятся на
делятся на  .
.
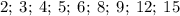 являются делителем
являются делителем 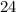 и
и 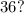
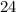 и
и 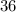 одновременно делятся на
одновременно делятся на 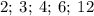 , ибо их конечные цифры чётные, суммы цифр этих чисел делятся на
, ибо их конечные цифры чётные, суммы цифр этих чисел делятся на  , их
, их  последние цифры образуют числа, делящиеся на
последние цифры образуют числа, делящиеся на  .
.
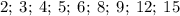 являются делителем
являются делителем 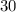 и кратным
и кратным 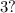
Требования к заданию: 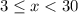 , где
, где  - искомые числа. Число
- искомые числа. Число  уже не подходит.
уже не подходит.
Числа 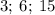 являются делителями
являются делителями 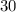 и кратны
и кратны  , ибо сумма цифр числа
, ибо сумма цифр числа 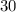 делится на
делится на  , последняя цифра
, последняя цифра  и она чётная.
и она чётная.
Пошаговое объяснение:
вот тут два ответа на выбор