Question

Запишите математические выражения в виде предложений с тематических терминов «сумма», «разность», «произведение», «частное
a) a+b+ 12;
б) (2 +a)(b-с);
в)100 - (х+у);
г) 4m - 8;
д) 6k + 3);
е) а - с;
а+ь
ж) 2 + 4,5b;
и) (n -7).
Parece​

Answer 1

a) a+b+ 12

Сумма a, b и 12.

б) (2 +a)(b-с);

Произведение суммы 2 и а и разности b и с.

в)100 - (х+у);

Разность 100 и суммы x и y.

г) 4m - 8;

Разность произведения 4 и m и 8.

д) 6k + 3);

Предположу, что левая скобка стоит так: 6(k + 3)

Произведение 6 и суммы k и 3.

Если же правильная запись 6k + 3, то это сумма произведения 6 и k и 3.

е) а - с;

а+b

Предположу, что здесь имелась в виду эта дробь: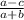 $\frac{a-c}{a+b}$

Частное разности a и c и суммы a и b&

ж) 2 + 4,5b;

Сумма 2 и произведения 4,5 и b&.

и) (n -7).

Разность n и 7.