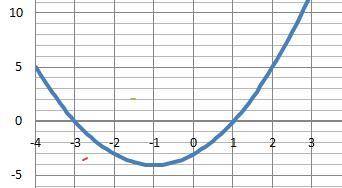
ДАНО: y(x) = x² + 2*x - 3
ИССЛЕДОВАНИЕ
1. Область определения. Непрерывная. Разрывов нет.
D(y) = (-∞;+∞) , D(y) = R.
2. Нули функции, корни квадратного уравнения.
х₁ = - 3 и х₂ = 1.
3. Интервалы знакопостоянства.
Положительна: Y>0 X∈(-∞;-3)∪(1;+∞) - вне корней.
Отрицательна: Y<0 X∈(-3;1) - между корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 2*х + 2 = 2*(x + 1) = 0
Точка экстремума: x = - 1
5 Локальный экстремум: Ymin(-1) = - 4
6. Интервалы монотонности.
Убывает: Х∈(-∞;-1) Возрастает: Х∈(1;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 2.
8. Вогнутая - "ложка" - Х∈(-∞;+∞).
9. Область значений: E(y)= [-4;+∞)
График на рисунке в приложении.
Пошаговое объяснение:
ну получается, 11/24 и 3/10 приводим к общему знаменателю получается 55/120 и 46/120и получается 11/24 больше чем 3/10; 11/17 и 11/25 11/17 больше чем 11/25, так как когда числительные одинаковые, то где знаменатель меньше, та дробь больше;15/16 и 15/25больше та дробь где знаменатель меньше, так как одинаковые числительные; 5/6 = 80/96, 31/32=93/96, поэтому 5/6 меньше чем 31/32