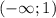Пусть даны четыре отличных от нуля числа a, b, c и d таких, что a : b = c : d. тогда равенство a : b = c : d называется пропорцией. т.е. пропорция(лат. proportio — соразмерность, выравненность частей) — равенство двух отношений. числа a и d называются крайними членами пропорции, а числаb и c — средними членами. пишут, a : b = с : d или читают: «а так относится к b, как с относится к d» из свойств обыкновенных дробей следует, что справедливы следующие утверждения: пропорцию a : b = c : d можно записать в виде a/b = c/d.крайние члены пропорции можно поменять местами: если a/b = c/d, то d/b = c/a.средние члены пропорции можно поменять местами: если a/b = c/d, то a/c = b/d.произведение крайних членов пропорции равно произведению её средних членов: если a/b = c/d, то ad = bc (основное свойство пропорции). например: если 20: 5 = 16: 4, то 20•4 = 5•16, т.е. 80=80.
a)f(x)=-8x^2-2x+1
f'(x)=-8*2x-2*1=-16x-2
-16x-2>0
-16x>2
x<-2/16
x<-1/8
b)f(x)=1+x-6x^2
f'(x)=1-6*2x=1-12x
1-12x>0
-12x>-1
12x<1
x<1/12
c)f(x)=(x^3/3)-(x^2)+2
f'(x)=1/3 * 3x^2 -2*x=x^2 - 2x
x^2 - 2x>0
x^2 - 2x =0
x(x-2)=0
x=0 x=2
Чертим координатную прямую и отмечаем точки, расставляем знаки.
___+______-______+_____
0 2
Решением неравенства является промежуток
d)f(x)=((-x^3)/3)- 1/2x^2+6/7
f'(x)=-1/3 * 3x^2 - 1/2 * (-2)* 1/x^3 =-x^2 +1/x^3
-x^2 + 1/x^3 >0
Домножим на x^3:
-x^5 +1>0
-x^5>-1
x^5 < 1
x<1
Решением будет являться промежуток