Задача.
а=14 см.
b=1\2 от 14
1)14/2=7(см)-Ширина
P-?см.
P-a+b+a+b P-14+7+14+7=42(cм)
a=8 см. 2 мм=82 мм
b=1/2 от 82 мм.
1)82/2=41(мм)-ширина
P-?см
P-a+b+a+b
P-82+41+82+41=246(см)
a=20м
b=1|2 от 20 м
1)20/2=10(м)-ширина
P-?см
P-a+b+a+b
P-20+10+20+10=60(м)
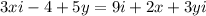

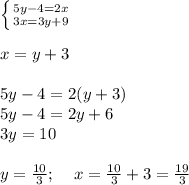

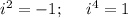
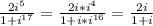
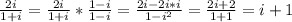
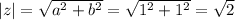
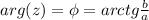
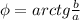


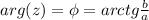
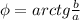
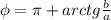
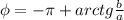
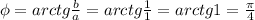
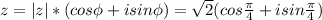
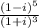
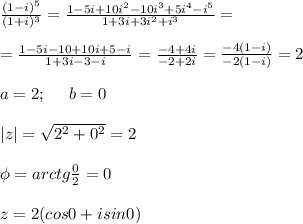
1) 14:2=7 см ширина
(14+7)*2=42 см периметр
2)82мм:2=41 мм ширина
(82+41)*2=246 мм периметр
3)20:2=10м ширина
(20+10)*2=60 м пеиметр