Пусть объем бассейна = V.
И пусть первая труба заполняет его за Т1 часов, а второя за Т2 часов.
Так как первая на 3 часа быстрее заполняет его то Т2=Т1+3
скорость заполнения 1 трубой = V/T1 а второй V/T2
за 2 часо первая заполнила объем 2 * (V/T1)
за 2 часо вторая заполнила объем 2 * (V/T2)
так как вдвоем они заполнили весть объем то 2 * (V/T1) + 2 * (V/T2) =V
преобразуем последнее уравнение
2 * (V/T1) + 2 * (V/T2) - V =0
V*( 2/T1 + 2/T2 - 1) =0 ==> 2/T1 + 2/T2 - 1 =0
подставим в него выражение для Т2 (Т2=Т1+3) получим
2/T1 + 2/(Т1+3) - 1 =0
приводим к общему знаменателю
[2*(Т1+3) + 2*T1 - T1*(Т1+3)] / [T1*(Т1+3)]=0 ===> 2*Т1+6 + 2*T1 - T1*Т1-3*T1 =0 ==>
==> T1^2 - T1 - 6 = 0
разложим на множители
T1^2 - T1 - 6 = (Т1+2)*(Т1-3)
(Т1+2)*(Т1-3)=0 ==> T1=-2 и T1=3
так как время не может быть отрицательным то получаем один ответ
первая труба заполнит за 3 часа
1.
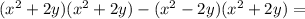

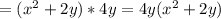
2.
a) 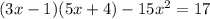


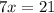

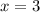
b) 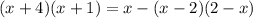
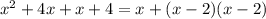

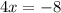


3. 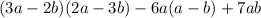 =
=

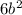
Чтобы найти значение выражения, надо знать
только значение переменной b.
ответ: 3) Только переменной b.
4.
Пусть х - цифра десятков, тогда
(12-х) - цифра единиц
получаем
10х+(12-х)= (9х+12) - данное двузначное число.
(12-х)*10+х= (120-9х) - обратное число к данному.
По условию: если к данному двузначному числу прибавить 54, то получится число, обратное данному.
Уравнение:
(9х+12) + 54 = (120-9х)
9х+9х = 120 -12-54
18х = 54
х = 54 : 18
х = 3 цифра десятков, тогда
12 - 3 = 9 - цифра единиц.
39 - данное двузначное число.
ответ: 39.
ответ:7,2
Пошаговое объяснение:
Тр-к АМN подобен тр-ку АВС, <А-общий,<N=<C (соответственные при MN||BC и секущей АС, тогда MN/BC=AM/AB, 3/BC=5/12, BC=36/5=7,2