Сумма длин двух сторон этого прямоугольника равна 180 м. Пусть длина одной стороны равна 
. Тогда длина второй равна 
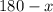. Площадь участка равна произведению длин сторон: 
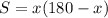. Рассмотрим эту площадь как функцию, найдём её производную и экстремум:
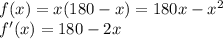
Приравняем производную к нулю, чтобы найти экстремум:
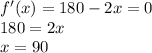
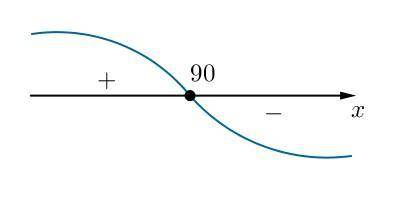
Методом интервалов (см. иллюстрацию) устанавливаем, что при прохождении через точку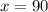 
производная меняет знак с плюса на минус. Это значит, что 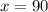— точка максимума.
Это означает, что длины сторон этого прямоугольника должны быть равны, то есть это квадрат со стороной длиной 90 м. Его площадь равна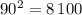 
м²
ответ: 8 100 м²
х≠-1, все остальные х в основании подходят. основание больше единицы, поэтому при х≠-1
(х²+3х+2)/(х²-3х+4)>0
(х²+3х+2)/(х²+3х+2)≤1
Решаем первое неравенство. оно строгое. По Виету корни числителя -1 и -2; и дискриминант знаменателя меньше нуля, старший коэффициент положителен, D= 9-16 отрицат., значит, знаменатель положителен всегда.
тогда ОДЗ
___-2-1 х∈(-∞;-2)∪(-1;+∞)
+ - +
второе неравенство (х²+3х+2)/(х²-3х+4)≤1;
(х²+3х+2)/(х²-3х+4)-1≤0;после приведения к общему знаменателю сократим уравнение на положительную величину (х²-3х+4),
х²+3х+2-(х²-3х+4)≤0; 3х+2+3х-4≤0⇒6х≤2; х≤1/3
С учетом ОДЗ х∈(-∞;-2)∪ (-1;1/3]
По теореме Пифагора вычисляем гипотенузу =√(5²+12²)=13.
.
Формула для вычисления радиуса вписанной окружности по площади.
S=1/2 *P*r, где Р - периметр, а r - радиус вписанной окружности.
r=S/( 1/2 P) - Вычисляем площадь по основанию 12 и высоте 5.
S= 1/2 * 12 * 5 =30 - и определяем радиус.
r=30 / ( 1/2(5+12+13) = 30/15=2 см.
.
Есть формула для этого радиуса по сторонам.
r=(a+b-c)/2 = (5+12-13)/2=2 см.