 - Количество коробок с яблоками
- Количество коробок с яблоками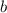 - Количество коробок с грушами
- Количество коробок с грушами - Количество коробок с персиками
- Количество коробок с персиками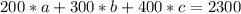
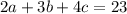
 ). Для этого выразим из уравнения эту переменную:
). Для этого выразим из уравнения эту переменную: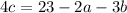
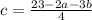
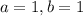 ). Это значение равно 5.
). Это значение равно 5. 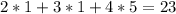
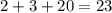
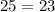 - это неверно, поэтому нужно уменьшить количество коробок с персиками на 1 штуку и получим 4 коробки.
- это неверно, поэтому нужно уменьшить количество коробок с персиками на 1 штуку и получим 4 коробки.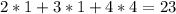
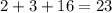
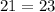 - это верно. У нас даже есть остаток равный 23-21=2, а так как мы делили вначале на 100, то здесь нужно умножить на это число. Получим остаток равный 200 рублей. На них мы можем купить еще 1 коробку с яблоками по цене 200 рублей. И тогда все деньги будут потрачены, что и необходимо по условию задачи.
- это верно. У нас даже есть остаток равный 23-21=2, а так как мы делили вначале на 100, то здесь нужно умножить на это число. Получим остаток равный 200 рублей. На них мы можем купить еще 1 коробку с яблоками по цене 200 рублей. И тогда все деньги будут потрачены, что и необходимо по условию задачи.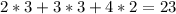
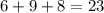
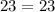
Вот ответ на фото. Надеюсь лучший ответ